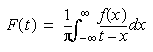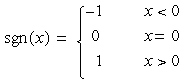The Hilbert transform of a function f(x) is defined by:

Theoretically, the integral is evaluated as a Cauchy principal value. Computationally one can write the Hilbert transform as the convolution:

which by the convolution theorem of Fourier transforms, may be evaluated as the product of the transform of f(x) with -i*sgn(x), where:

The Hilbert transform can be considered to be a filter which simply shifts phases of all frequency components of its input by -π/2 radians.

An "analytic" (complex time) signal Y(t) can be constructed from a real-valued input signal y(t):

• Y(t) = y(t) + j h(t)

where,

• Y(t) is the analytic signal constructed from y(t) and its Hilbert transform
• y(t) is the input signal
• h(t) is the Hilbert Transform of the input signal

The real and imaginary parts can be expressed in polar coordinates as:

• Y(t) = A(t) exp[jψ(t)]

where,

• A(t) is the "envelope" or amplitude of the analytic signal
• ψ is the phase of the analytic signal (the derivative of ψ is called the "instantaneous frequency")

These Igor Pro® commands compute a signal´s "envelope" using the HilbertTransform operation:

	HilbertTransform inputSignal	// creates W_Hilbert
	Rename W_Hilbert, envelope
	envelope= real(r2polar(cmplx(inputSignal[p], envelope[p])))

Note that the Hilbert transform of a constant is zero. If you compute the Hilbert transform in more than one dimension and one of the dimensions does not vary (is a constant), the transform will be zero (or at least numerically close to zero).

Igor´s HilbertTransform operation computes the Hilbert transformation of real or complex (single or double precision) data of 1-3 dimensions.

References

• Bracewell, R., The Fourier Transform and Its Applications, McGraw-Hill, 1965.
• Feldman, M., "Non-linear system vibration analysis using Hilbert Transform - I. Free Vibration Analysis Method 'FREEVIB'", Mechanical Systems and Signal Processing (1994) 8(2), 119-127.