What parameters best characterize a cluster in a 2-D data set?

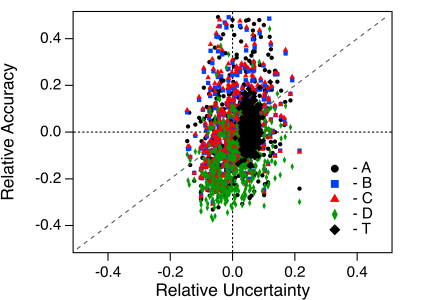
I am comparing output performance on test cases. The two parameters that I track as output performance are relative accuracy RA and relative uncertainty RU. I show an example plot for distributions obtained plotting RA versus RU from 900 samples in each of five different test cases I would like to obtain parametric measures on the distributions to chart the five cases.

The samples are brute force curve fitting to five different equations that should fit a data set. The T form is the non-linear regression fitting. The A - D forms are linearized fitting models. I generate raw theory, add Gaussian noise to the raw data, and perhaps chop out a front end portion of the data as computational ways to mimic experimental approaches to obtain the data. I envision mapping perhaps three parameters for each of the five clusters. I think about this as plotting three characters of a "best fit" ellipse ... centroid (center of mass), aspect, and rotation.

I am hitting the wall of my complete ignorance on the best approach here. Recommendations would be greatly appreciated.