
fitting parameters for a system of differential equations
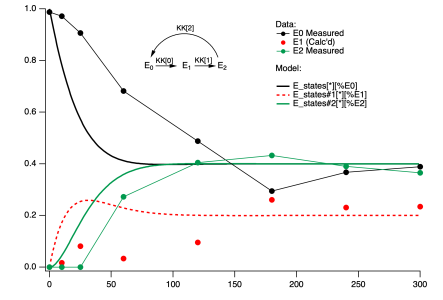
I have defined a system of differential equations controlled by three parameters. it describes the time evolution of 3 species defined by 3 rate constants KK[0], KK[1] and KK[2]. The model is supposed to describe data that is presented in graph zero as lines and markers (the data describes the species labeled E0 and E2. E1, in this case, is just obtained by assuming E0 + E1 + E2 = 1). my goal here is to vary the KK parameters to get as close as possible to the data. ( I realize the fit will may not be great, and getting a good fit may require a more sophisticated model, just want to see how closely this model can fit) How can i do this with Igor? ihave attached the relevant pxp file which has all the data and the model in it.

Forum

Support
Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More







Fitting two components is a bit tricky, start by fitting one component. I've looked at your experiment file and I'm a little bit confused about your intentions; it looks like you started from the fit function in the Differential Equation Demo experiment, which is too simple for your case.
You have three rate constants- if they are independent, then you have three fit coefficients just for the rate constants. It looks like the initial conditions are simply E0=1, E1=E2=0, so no need to put those into the fit coefficients. It's not clear that you need fit coefficients other than your rate constants. Here is a possible fit function for fitting the third component:
A flexible but inefficient way to fit the first and third components would be to write two fit functions, one for each component. Then use the Global Fit package to fit the two components together. That will evaluate the ODE twice as many times as necessary, though.
Another way to fit two components would be to concatenate the two components into a single wave, one after the other. The wave would have 2N components, the first N would be the first component, the second N would be the third component. You also need to make an X wave that has all the X values twice, one set for the first component, one for the third. The fit function might look like this:
FuncFit doesn't know that your fit function expects two data sets in the yw wave, so the /D (autodestination) doesn't work. You can use /D=destwave, though, because all the numbers of points and point order will Just Work that way.
Good luck with this project, and feel free to ask more questions. I guarantee you will have more :)
March 26, 2020 at 02:11 pm - Permalink
Dear All,
I found this topic very useful regarding the data analysis I am currently doing on enzymatic reactions monitored using fluorophores.
@johnweeks, you propose a fitting function in which the number of points of the ODEsolution is identical to the one of the data set wave. Would the quality of the fit better with a higher number of points in the ODEsolution ?
In that spirit, I was trying the following:
Here I am using xw (which define the total experimental observation time from 0 to x seconds) to create a reference wave that will be used as x-axis values during the numerical integration.
Unfortunately the scaling along the x (temporal) axis seemed to be wrong so I guess that I did a mistake. Maybe you can comment on that ?
Thank a lot.
April 17, 2020 at 05:58 am - Permalink
Integrating at a finer X resolution will not help the quality of the solution. Internally, IntegrateODE adjusts step size to maintain the requested accuracy estimate. It will take as many steps between your X values as are required to maintain accuracy.
The error in your code is using [p] on the right-hand side of the final wave assignment. You need to use the values from xw:
yw = ODEsolution(xw[p])[3]April 17, 2020 at 11:03 am - Permalink
Thank a lot ! I to your explanation regarding the number of points. So I do not need to increase it to get better results.
For the code I guess you meant:
April 17, 2020 at 12:13 pm - Permalink
No, I really meant xw[p].
The reason is that the X values where you need to fill in yw are in the wave xw. The [p] means to use the point numbers from the left side of the wave assignment; xw[p] is the correct X value for the point in yw. Using () for indexing the rows of ODEsolution means to index by scaled X value rather than by point numbers.
April 17, 2020 at 03:50 pm - Permalink
Perfect thanks a lot.
April 18, 2020 at 12:05 am - Permalink