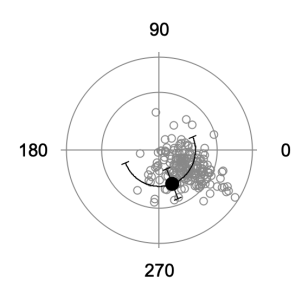
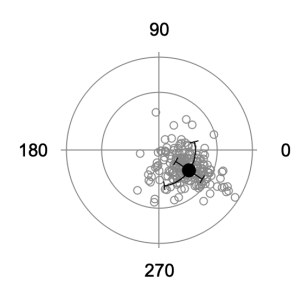
Polar averaging and errors

Function polarAvgErr(inWave,opStr,degrad)
    Wave inWave //single wave with list of angles
   
    //opStr = "avg", "sdev", or "sem"
    //degrad = "deg" or "rad" depending on the input data type
    String opStr,degrad
    Variable i,size,avgX,avgY,avg,sdev,sem,errX,errY,value,multiplier
   
    size = DimSize(inWave,0)
    Make/FREE/N=(size) xTotal,yTotal
       
    //input is degrees or radians
    strswitch(degrad)
        case "deg":
            xTotal = cos(inWave * pi/180)
            yTotal = sin(inWave * pi/180)
            multiplier = 180/pi
            break
        case "rad":
            xTotal = cos(inWave)
            yTotal = sin(inWave)
            multiplier = 1
            break
    endswitch

    //polar average
    avgX = mean(xTotal)
    avgY = mean(yTotal)
    avg = atan2(avgY,avgX)*multiplier
   
    If(avg < 0)
        avg += 360
    EndIf
   
    //polar standard deviation
    For(i=0;i<size;i+=1)       
        errX += (xTotal[i] - avgX)^2/(size-1)
        errY += (yTotal[i] - avgY)^2/(size-1)
    EndFor
   
    errX = sqrt(errX)      
    errY = sqrt(errY)
    sdev = atan2(errY,errX)*multiplier
           
    //polar standard error of the mean
    sem = sdev/sqrt(size)
   
    //select return parameter
    strswitch(opStr)
        case "avg":
            value = avg
            break
        case "sdev":
            value = sdev
            break
        case "sem":
            value = sem
            break
    endswitch
   
    return value
End