LogNormal Multipeak Fitting Asymmetric Data

Share icon

I've been having trouble with the default log normal fitting function in both base igor pro 8 and the multipeak fitting package. Specifically, the regular fit will not skew, even though I have asymmetric spectroscopic data. I ended up programming my own log normal function that does allow for a skewed fit, and it does work. However, I've been unable to figure out how to get the data I want - area and peak maximum location - out of the multipeak fitting package. Additionally, the peaks aren't showing up in the individual peak section of the multipeak fitting graph, and when I try to put them in their own graph window, they don't look like a log-normal fit.

If someone can tell me either how to get the default multipeak lognormal fit function to fit asymmetric data, or how to get my function properly working with the multipeak fitting package, that would be very helpful. Thanks!

//This is the peak function - the actual fitting function
Function MRGLogNormal(w, yw, xw)
    Wave w
    Wave yw, xw
    
    Variable l = w[0]
    Variable b = w[1]
    Variable h = w[2]
    Variable a = w[3]
    
    yw = (h/(xw*a*sqrt(2*pi)))*exp(-((ln(xw-l)-b)^2)/(2*a^2))
    
end

 

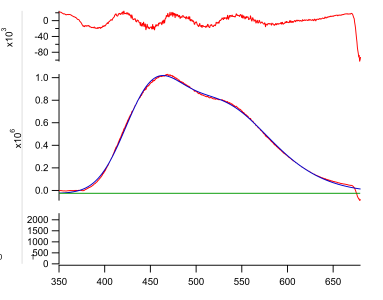
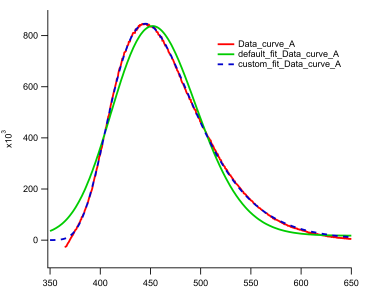
 Multiple peaks fitted to a custom log normal function Single peak fitted to both the default and a custom log normal function Multipeak fitting lognormal problem 6-3-25.pxp (838.29 KB) MRG_LogNormal.ipf (2.88 KB)

First, the lognormal function in multipeak fitting (MPF) is symmetric, so you cannot introduce a skew here. Also, I think upgrading to Igor 9 will make your life much easier, because the MPF package received a huge update. I have looked only briefly into your fit data. I can see where the issues are but I have a few questions:

  • Is it necessary to fit this specific function to your data and a generic asymmetric function (such as ExpModGauss) will not do?
  • Where did you find this function (is there a definition somewhere to look at)? None of the parameters seem to indicate the peak location, i.e., are even remotely close to the peak 'maximum'. This will not work well with MPF, as you have already found out. At least it would be necessary to reformulate the Start Location (l) into a peak location parameter.
  • For outputting the peak location, height, fwhm, area etc. ideally you want a mathematical derivation of these parameters. Are there equations for any of these parameters for your peak shape? Otherwise the only alternative is to get results numerically.

June 3, 2025 at 02:06 pm - Permalink

I looked at your equations a bit more closely. I think a modified version would work:

Function MRGLogNormal_asym(w,x) : FitFunc
    Wave w
    Variable x
 
    //CurveFitDialog/ These comments were created by the Curve Fitting dialog. Altering them will
    //CurveFitDialog/ make the function less convenient to work with in the Curve Fitting dialog.
    //CurveFitDialog/ Equation:
    //CurveFitDialog/ f(x) = h*exp(-( ln((x-l)/(b-l)) / (sqrt(2)*a) )^2)
    //CurveFitDialog/ End of Equation
    //CurveFitDialog/ Independent Variables 1
    //CurveFitDialog/ x
    //CurveFitDialog/ Coefficients 4
    //CurveFitDialog/ w[0] = a
    //CurveFitDialog/ w[1] = b
    //CurveFitDialog/ w[2] = h
    //CurveFitDialog/ w[3] = l
 
    if (x<=w[3])
        return 0
    else
        return w[2]*exp(-( ln( (x-w[3])/(w[1]-w[3]) )/( sqrt(2)*w[0] ) )^2)
    endif
End

With this your parameters a, b, h would actually be the width(?), position, height respectively. Such an equation could be implemented in Multipeak Fit and would give you a proper peak shape. I think it would also be possible to derive an analytical FWHM if you are good at calculus. Maybe even the already present equations of MPF can be reused if the equation is properly rescaled by l (w[3]) in the end.

June 3, 2025 at 08:43 pm - Permalink

Thanks very much for the help - I will definitely talk to my supervisor about upgrading to igor pro 9. The original log normal function I was using is actually a slightly modified version of the one from the help page for the multipeak function package - I've attached a screenshot below. According to that help file, I believe width = a * sqrt(2)

I do have one follow up question - I was able to implement your fitting function into multipeak fit as follows, but the peaks are still displaying incorrectly in the window, as well as when I open them in a new graph. Is there a way to fix this that I am overlooking? 

Function MRGLogNormal(w, yw, xw)
    Wave w
    Wave yw, xw
    
    Variable i
    
    for(i=0;i<numpnts(xw);i+=1)
        if (xw[i]<=w[3])
            yw[i]=0
        else 
            yw[i] = w[2]*exp(-( ln( (xw[i]-w[3])/(w[1]-w[3]) )/( sqrt(2)*w[0] ) )^2)
        endif       
    endfor
 
end

 
Multipeak fitting help file lognormal equation (64 KB) Multipeak fitting data problem with peaks (48.47 KB)

June 4, 2025 at 07:05 am - Permalink

I think the remaining issue is that MPF expects a certain order of parameters. Rewrite your fit function to have the following order of parameters: 0 - position, 1 - width, 2 - height, 3 - other (shape in this case?. You can also share your code and I can have a look tomorrow.

June 4, 2025 at 07:26 am - Permalink