
Translating MatLab matrix multiplications to Igor Pro?
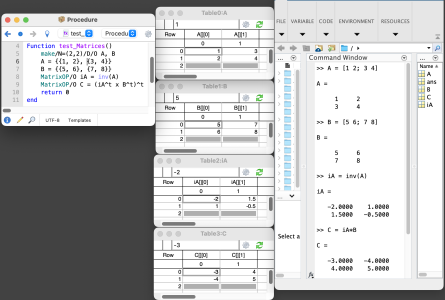
I am working on a project that requires me to map MatLab matrix multiplication operations into Igor Pro. I am trying to wrap my head around the proper way to do this with MatrixOP. The attached image shows a use case to obtain C = inv(A) x B. The left is Igor Pro. The right is MatLab. The only way I could get Igor Pro to create the comparable result to MatLab is by transposing each term in the multiplication and then transforming the result.
My question is whether I should now presume that this has to be the case for all matrix multiplication steps going from MatLab to Igor Pro. For example, if MatLab uses M = A x B x C, I should write MatrixOP/O M = (A^t x B^t x C^t)^t to obtain the comparable result?







As far as I can tell, Igor works exactly the same as matlab, but you need to make sure to write your input in the same way. Look how the row and columns of A and B in Igor are already flipped in your example. You should do:
Note how the inner brackets write columns, and thus the numbers are not arranged in the same way in as Matlab, which writes in terms of rows.
June 29, 2023 at 06:47 am - Permalink
After playing around with this a bit, I came to the same conclusion as chozo. My only addition is that you can write it as
June 29, 2023 at 06:59 am - Permalink
An input A = {{1, 2}, {3, 4}} writes {1, 2} into the first ROW of a 2D WAVE. Writing (1 2; 3 4) into MatLab puts (1 2) into the first ROW in a 2D MATRIX. The terminologies for ROW and COLUMN are the same. **But** ... when you want results from 2D matrix math in Igor Pro to match results for 2D matrix math in MatLab, you must apply this rule:
(Igor Pro 2D WAVE)^t = (MatLab 2D Matrix)
Hence for example also the notes for using the /T flag on MatrixMultiply (and other commands).
I believe that we are all saying the same thing.
June 29, 2023 at 07:28 am - Permalink
JJ, I think we have a consistent answer now on how to translate MatLab to Igor, but I am curious why you think that the syntax {{a},{b}} writes rows, when it does clearly not. You can see from the table that A = {{1, 2}, {3, 4}} writes 1,2 in the first column, not row. Maybe have a read of:
There you can find for example:
So, I would not agree that (Igor Pro 2D WAVE)^t = (MatLab 2D Matrix), but rather in terms of syntax {{1, 2}, {3, 4}} != (1 2; 3 4). I would be curious where in the Igor help this is contradicted. Anyway, I don't want to insist on anything here. I am just wondering whether you are accidentally confusing the syntax, which would clear up everything.
June 29, 2023 at 08:13 am - Permalink
The convention in a wave is row, column, layer, chunk. A 2D wave displayed in an edit table by default shows rows vertical and columns horizontal.
One difference is: By default, a ROW in Igor Pro displays vertically in a table, while by default a ROW in MatLab displays horizontally.
With MatrixOP (and apparently with Matrix... math commands), matrix math on 2D waves appears to follow the convention that a matrix ROW runs along the horizontal direction *even tough this is a COLUMN in the 2D wave convention*.
Perhaps this is the source of the confusion.
June 29, 2023 at 09:23 am - Permalink
To clear some of the confusion let's return to history.
Originally Igor supported 1D waves only. They were displayed in a table as one column per wave. When Igor was extended to support multi-dimensional waves they were formed by adding columns and so a contiguous array of 256 points can represent a 2-column 2D wave of 128 rows or a 4-column array of 64 rows and you can use Redimension to go between these representations.
One area where this caused confusion is that when you display a 2D wave in a table, the x-scaling applies to the vertical axis and the y-scaling applies to the horizontal axis. The same applies to the display of a matrix as an image.
I take no credit for this formulation and I confess that it caused me grief in Igor's image-processing applications.
Well-designed software libraries generally allow you to specify if your data is packed as column-major (as in Igor) or row-major. Igor is strictly column-major despite what may appear otherwise when it comes to printing or initializing a wave with an array of constants.
For alternate storage representation (and a superb way to get a headache) you can check out the options available under MatrixSparse.
Also, I tend to think that the use of ^t is probably unnecessary.
A.G.
June 29, 2023 at 04:30 pm - Permalink
Thanks AG. No end of grief is never a good place to be.
In summary, here are the MatLab and Igor Pro syntaxes that apply when entering data into a 2x2 matrix, where r is row and c is column
MatLab A = (r1c1 r1c2; r2c1 r2c2)
Igor Pro A = {{c0r0, c0r1}, {c1r0, c1r1}}
I imagine this means that MatLab is row-major in your designation. One has two options to translate matrix data from MatLab -> Igor Pro for subsequent matrix math operations.
* Transcribe manually between row-major representations in MatLab and column-major representations in Igor Pro as one enters or creates the matrix.
* Enter data directly as MatLab -> Igor Pro (r1c1 r1c2; r2c1 r2c2) -> {{r1c1, r1c2}, {r2c1, r2c2}} and use ^t.
Matlab C = A*B
Igor Pro MatrixOP C = (A^t x B^t)^t // note the matrix "x" rather than the math "*" symbol here!!
I had a MatLab script with matrices to translate. I chose to work with the second approach. My brain is no longer resilient enough to translate index notations between rows and columns manually even for a simply case of a 2x2 matrix. The easier (brute force) approach was to add the ^t notation throughout MatrixOP commands in Igor Pro until my resultant output matrix in Igor Pro matched what the resultant output matrix in MatLab (albeit with columns and rows transcribed).
I've since run across two other cases where I had to pay attention to index representations in translating a MatLab matrix operation to an Igor Pro MatrixOP operation. In one case, I avoided ^t by recognizing the transcription manually and in the other case I used ^t to convert a row vector to a column array (for graphing).
MatLab rv = M(2,1)/M(1,1) --> Igor Pro rv[0][] = M[0][1][q]/M[0][0][q]
MatLab rreal = rv * conj(rv) --> Igor Pro MatrixOP/O rreal = real( (rv * conj(rv))^t )
At least with this, my grief has ended (for now).
June 30, 2023 at 10:11 am - Permalink