How to compute and display scalp potentials from EEG recordings

Created on July 7 at 12:34 pm - by: admin

EEG researchers commonly create spatial maps of the electrical activity acros the scalp. Data are interpolated or triangulated from a discrete number of electrode placements distributed across the scalp (generally greater than 32 sites) often in fixed/standardized positions (see, e.g., http://www.ant-neuro.com/products/waveguard_original).

To do this, electrode coordinates, either as {x, y, z} triplets or in spherical coordinates are needed and can be obtained from the manufacturer of electrode caps (e.g., https://www.egi.com/knowledge-center/item/71-sensor-position-files-for-visualizing-data-in-third-party-software).

Theoretical analysis typically involves modeling the head as a perfect sphere. The mapping of the electrode coordinates to the surface of a sphere can be accomplished with the following function:

Function scaleToSpherical(inWave)
    Wave inWave
    
    // offset the coordinates to the  origin:
    MatrixOP/o/free wave0c=subtractMean(inWave,1)
    
    // compute the distance of electrodes from the origin:
    MatrixOP/O/free rawRad=sqrt(magsqr(col(wave0c,0))+magsqr(col(wave0c,1))+magsqr(col(wave0c,2)))
    
    // rescale the distance to a radius of 1:
    MatrixOP/O centeredNormalized=scalerows(wave0c,rec(rawRad))
End

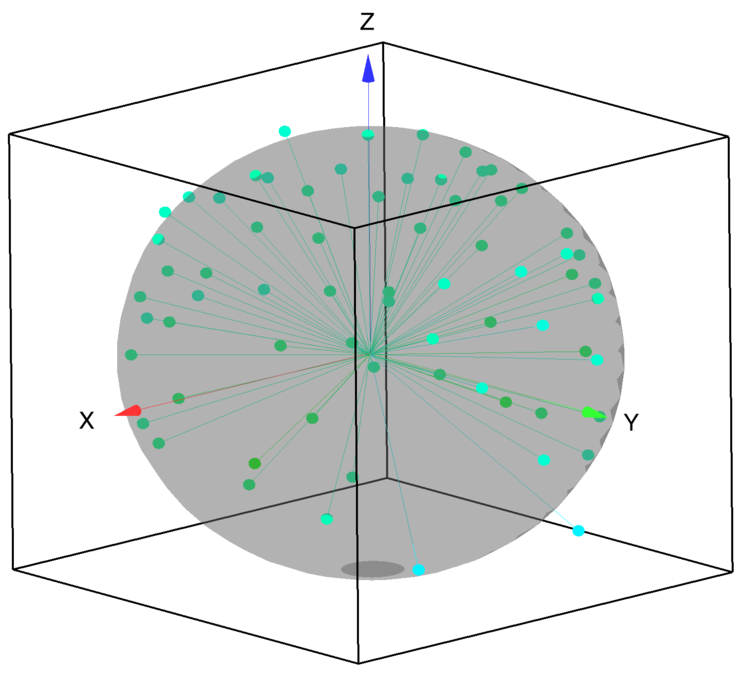
Figure 1: Initial electrode positions relative to the surface of a sphere.

Figure 1:Initial electrode positions relative to the surface of a sphere.

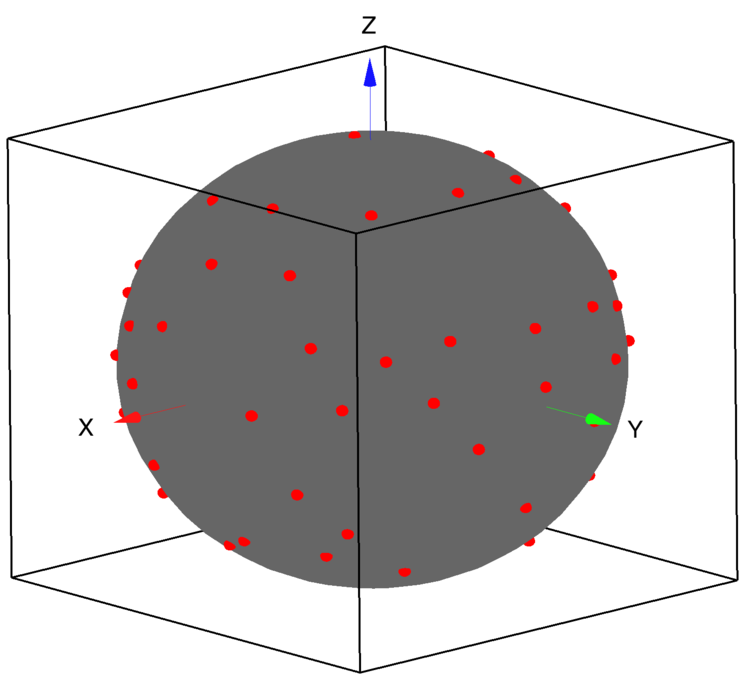
Figure 2: Normalized electrode coordinates on the surface of a sphere.

Figure 2: Normalized electrode coordinates on the surface of a sphere.

Using the normalized set of coordinates we can triangulate the data on the surface of a sphere using the SphericalTriangulate operation.

SphericalTriangulate centeredNormalized // this creates M_TriangulationData

Following the triangulation we can use the wave M_TriangulationData combined with the EEG data to interpolate the potentials at any point on the sphere. In order to display the resulting interpolation in Gizmo we start by creating a parametric surface representing the sphere.

Function makeParametricSphere(pointsx,pointsy)
    Variable pointsx,pointsy
    
    Variable i,j,rad
    Make/O/N=(pointsx,pointsy,3) parametricW
    Variable anglePhi,angleTheta
    Variable dPhi,dTheta
    
    
    dPhi=2*pi/(pointsx-1)
    dTheta=pi/(pointsy-1)
    Variable xx,yy,zz
    Variable sig
    
    for(j=0;j<pointsy;j+=1)
        angleTheta=j*dTheta
        zz=sin(angleTheta)
        if(angleTheta>pi/2)
            sig=-1
        else
            sig=1
        endif
        for(i=0;i<pointsx;i+=1)
            anglePhi=i*dPhi
            xx=zz*cos(anglePhi)
            yy=zz*sin(anglePhi)
            parametricW[i][j][0]=xx
            parametricW[i][j][1]=yy
            parametricW[i][j][2]=sig*sqrt(1-xx*xx-yy*yy)
        endfor
    endfor
End

To complete the interpolation we need to construct one more wave: dataPointsWave. This wave has 4-columns consisting of the electrode coordinates in the first three columns and the potentials measured by each electrode at some fixed time t0 in the fourth column:

Variable nRows=DimSize(centeredNormalized,0)
    Make/O/D/N=(nRows,4) dataPointsWave
    dataPointsWave[][0,2]=centeredNormalized
    dataPointsWave[][3]=electrodePotentials[p]

The interpolation is computed by:

SphericalInterpolate M_TriangulationData,dataPointsWave,sphereData

The resulting interpolation is stored in the wave W_SphericalInterpolation where each row contains the scalar potential interpolated for the corresponding XYZ location in the wave sphereData. To display these values on the parametric surface we need to construct a color wave

Function createParametricColorWave(pWave,interpWave,reverseCTAB)
    Wave pWave,interpWave
    Variable reverseCTAB            // set to 1 to reverse; 0 otherwise
    
    // the color wave must match the parametric surface:
    Variable rows=dimsize(pwave,0)
    Variable cols=dimSize(pWave,1)
    
    // Create the parametric color wave:
    Make/O/N=(rows,cols,4) pWaveColor=1     
    
    // find the range of values for scaling:
    Variable mmax=WaveMax(interpWave)
    Variable mmin=WaveMin(interpWave)
    
    // optionally replace the colortable here:
    ColorTab2Wave rainbow256
    Wave M_Colors
    // not all colortables have the same number of colors:
    Variable nTableCols=DimSize(M_Colors,0)-1
 
    if(reverseCTAB)
        MatrixOP/o/free aa=col(M_Colors,0)
        WaveTransform/o flip aa
        MatrixOP/O M_Colors=setCol(M_Colors,0,aa)
        MatrixOP/o/free aa=col(M_Colors,1)
        WaveTransform/o flip aa
        MatrixOP/O M_Colors=setCol(M_Colors,1,aa)
        MatrixOP/o/free aa=col(M_Colors,2)
        WaveTransform/o flip aa
        MatrixOP/O M_Colors=setCol(M_Colors,2,aa)
    endif
    
    MatrixOP/O M_Colors=fp32(M_Colors/65535)
    Variable nor=nTableCols/(mmax-mmin)
    Variable i, np=rows*cols,index,rr,cc
    for(i=0;i<np;i+=1)
        index=trunc((interpWave[i]-mmin)*nor)
        rr=mod(i,rows)
        cc=trunc(i/rows)
        pWaveColor[rr][cc][0]=M_Colors[index][0]
        pWaveColor[rr][cc][1]=M_Colors[index][1]
        pWaveColor[rr][cc][2]=M_Colors[index][2]
    endfor
End

An example of this approach is illustrated in a cross-lingustic speech discrimination study at the following webpage:

http://www.gc.cuny.edu/Page-Elements/Academics-Research-Centers-Initiatives/Doctoral-Programs/Speech-Language-Hearing-Sciences/Research-Labs/Developmental-Neurolinguistics-Laboratory/Research-Highlights

Valerie L. Shafer, Ph.D.
vshafer@gc.cuny.edu
Professor and Deputy Executive Officer
Ph.D. Program in Speech-Language-Hearing Sciences
The Graduate Center, CUNY
365 Fifth Avenue, NY, NY 10016

Blog Posts Igor Pro 7

Forum

Support

Gallery

How to compute and display scalp potentials from EEG recordings

Igor Pro 10

Igor XOP Toolkit

Igor NIDAQ Tools MX