
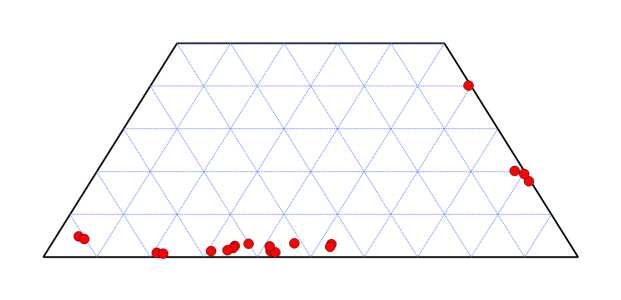
Cropped ternary diagram template
Snippet to generate a ternary diagram template. The ternary can be "full" or cropped, such that the top corner can be truncated at fractional values from 0.3 to 0.7 (in 0.1 increments). Cropping below or above that doesn't make much sense to me, but it could easily be added.
The function ConvMatrix2Ternary(M_Data) converts a 3-column data matrix in to a 2-column converted matrix that is compatible with ternary coordinates.
EDIT Jan 22nd 2019:
The initial code below contained a bug: The diagram coordinates and grid points need to be converted by multiplying the values of M_TernaryTemplate with cos(30*pi/180) and not, as initially posted, by dividing it. This has been fixed below. Sorry for any inconvenience.
function MakeTernaryTemplate([variable crop]) // was crop specified? If not, default is the full ternary crop = ParamIsDefault(crop) ? 10 : Crop*10 // aspect ratio of the ternary plot variable aspectRatio switch(crop) case 10 : Make/D/O/N=(37,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.5,0} M_TernaryTemplate[0][1]= {0,0,1,0} M_TernaryTemplate[0][2]= {0.05,0.1,0.55,0.45,0.9,0.95,0.05,NaN,0.1,0.2,0.2,0.6,0.4,0.8,0.9,0.1,NaN,0.15,0.3,0.65,0.35,0.7,0.85,0.15,NaN,0.2,0.4,0.7,0.3,0.6,0.8,0.2,NaN,0.25,0.5,0.75,0.25} M_TernaryTemplate[0][3]= {0.1,0,0.9,0.9,0,0.1,0.1,NaN,0.2,0,0,0.8,0.8,0,0.2,0.2,NaN,0.3,0,0.7,0.7,0,0.3,0.3,NaN,0.4,0,0.6,0.6,0,0.4,0.4,NaN,0.5,0,0.5,0.5} aspectRatio = 1.25 break case 3 : Make/D/O/N=(44,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.85,0.15,0} M_TernaryTemplate[0][1]= {0,0,0.3,0.3,0} M_TernaryTemplate[0][2]= {0.05,0.95,NaN,0.1,0.9,NaN,0.15,0.85,NaN,0.05,0.1,0.25,NaN,0.1,0.2,0.35,NaN,0.15,0.3,0.45,NaN,0.25,0.4,0.55,NaN,0.35,0.5,0.65,NaN,0.45,0.6,0.75,NaN,0.55,0.7,0.85,NaN,0.65,0.8,0.9,NaN,0.75,0.9,0.95} M_TernaryTemplate[0][3]= {0.1,0.1,NaN,0.2,0.2,NaN,0.3,0.3,NaN,0.1,0,0.3,NaN,0.2,0,0.3,NaN,0.3,0,0.3,NaN,0.3,0,0.3,NaN,0.3,0,0.3,NaN,0.3,0,0.3,NaN,0.3,0,0.3,NaN,0.3,0,0.2,NaN,0.3,0,0.1} aspectRatio = 3 break case 4 : Make/D/O/N=(47,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.8,0.2,0} M_TernaryTemplate[0][1]= {0,0,0.4,0.4,0} M_TernaryTemplate[0][2]= {0.05,0.95,NaN,0.1,0.9,NaN,0.15,0.85,NaN,0.2,0.8,NaN,0.05,0.1,0.3,NaN,0.1,0.2,0.4,NaN,0.15,0.3,0.5,NaN,0.2,0.4,0.6,NaN,0.3,0.5,0.7,NaN,0.4,0.6,0.8,NaN,0.5,0.7,0.85,NaN,0.6,0.8,0.9,NaN,0.7,0.9,0.95} M_TernaryTemplate[0][3]= {0.1,0.1,NaN,0.2,0.2,NaN,0.3,0.3,NaN,0.4,0.4,NaN,0.1,0,0.4,NaN,0.2,0,0.4,NaN,0.3,0,0.4,NaN,0.4,0,0.4,NaN,0.4,0,0.4,NaN,0.4,0,0.4,NaN,0.4,0,0.3,NaN,0.4,0,0.2,NaN,0.4,0,0.1} aspectRatio = 2.85 break case 5 : Make/D/O/N=(50,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.75,0.25,0} M_TernaryTemplate[0][1]= {0,0,0.5,0.5,0} M_TernaryTemplate[0][2]= {0.05,0.95,NaN,0.1,0.9,NaN,0.15,0.85,NaN,0.2,0.8,NaN,0.25,0.75,NaN,0.05,0.1,0.35,NaN,0.1,0.2,0.45,NaN,0.15,0.3,0.55,NaN,0.2,0.4,0.65,NaN,0.25,0.5,0.75,NaN,0.35,0.6,0.8,NaN,0.45,0.7,0.85,NaN} M_TernaryTemplate[43][2]= {0.55,0.8,0.9,NaN,0.65,0.9,0.95} M_TernaryTemplate[0][3]= {0.1,0.1,NaN,0.2,0.2,NaN,0.3,0.3,NaN,0.4,0.4,NaN,0.5,0.5,NaN,0.1,0,0.5,NaN,0.2,0,0.5,NaN,0.3,0,0.5,NaN,0.4,0,0.5,NaN,0.5,0,0.5,NaN,0.5,0,0.4,NaN,0.5,0,0.3,NaN,0.5,0,0.2,NaN,0.5,0,0.1} aspectRatio = 2.5 break case 6 : Make/D/O/N=(53,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.7,0.3,0} M_TernaryTemplate[0][1]= {0,0,0.6,0.6,0} M_TernaryTemplate[0][2]= {0.05,0.95,NaN,0.1,0.9,NaN,0.15,0.85,NaN,0.2,0.8,NaN,0.25,0.75,NaN,0.3,0.7,NaN,0.05,0.1,0.4,NaN,0.1,0.2,0.5,NaN,0.15,0.3,0.6,NaN,0.2,0.4,0.7,NaN,0.25,0.5,0.75,NaN,0.3,0.6,0.8,NaN,0.4,0.7,0.85} M_TernaryTemplate[45][2]= {NaN,0.5,0.8,0.9,NaN,0.6,0.9,0.95} M_TernaryTemplate[0][3]= {0.1,0.1,NaN,0.2,0.2,NaN,0.3,0.3,NaN,0.4,0.4,NaN,0.5,0.5,NaN,0.6,0.6,NaN,0.1,0,0.6,NaN,0.2,0,0.6,NaN,0.3,0,0.6,NaN,0.4,0,0.6,NaN,0.5,0,0.5,NaN,0.6,0,0.4,NaN,0.6,0,0.3,NaN,0.6,0,0.2,NaN,0.6,0,0.1} aspectRatio = 2 break case 7 : Make/D/O/N=(53,4) M_TernaryTemplate = NaN M_TernaryTemplate[0][0]= {0,1,0.65,0.35,0} M_TernaryTemplate[0][1]= {0,0,0.7,0.7,0} M_TernaryTemplate[0][2]= {0.05,0.95,NaN,0.1,0.9,NaN,0.15,0.85,NaN,0.2,0.8,NaN,0.25,0.75,NaN,0.3,0.7,NaN,0.05,0.1,0.45,NaN,0.1,0.2,0.55,NaN,0.15,0.3,0.65,NaN,0.2,0.4,0.7,NaN,0.25,0.5,0.75,NaN,0.3,0.6,0.8,NaN,0.35,0.7} M_TernaryTemplate[44][2]= {0.85,NaN,0.45,0.8,0.9,NaN,0.55,0.9,0.95} M_TernaryTemplate[0][3]= {0.1,0.1,NaN,0.2,0.2,NaN,0.3,0.3,NaN,0.4,0.4,NaN,0.5,0.5,NaN,0.6,0.6,NaN,0.1,0,0.7,NaN,0.2,0,0.7,NaN,0.3,0,0.7,NaN,0.4,0,0.6,NaN,0.5,0,0.5,NaN,0.6,0,0.4,NaN,0.7,0,0.3,NaN,0.7,0,0.2,NaN,0.7,0,0.1} aspectRatio = 1.75 break default: DoAlert 0, "Sorry, that crop-value is not supported!" return -1 endswitch // convert Y (columns 1 and 3) to ternary coordinates variable factor = cos(30*pi/180) M_ternaryTemplate[][1] *= factor M_ternaryTemplate[][3] *= factor // display ternary if it doesn't exist DoWindow/F Ternary if(!V_flag) Display/N=Ternary M_TernaryTemplate[][1] vs M_TernaryTemplate[][0] ModifyGraph noLabel=2,axThick=0, rgb=(0,0,0), lsize(M_TernaryTemplate)=2 ModifyGraph margin=50 // append grid AppendToGraph M_TernaryTemplate[][3] vs M_TernaryTemplate[][2] ModifyGraph rgb(M_TernaryTemplate#1)=(16385,28398,65535), lstyle(M_TernaryTemplate#1)=1 endif ModifyGraph width={Aspect,aspectRatio} return 1 end function ConvMatrix2Ternary(M_Data) // M_Data needs to be organised: left [][0], right [][1], top[][2] of the ternary wave M_Data // Make temp wave: normalise in case it isn't and/or turn to fractions Duplicate/O/FREE M_Data, M_temp MatrixOP/FREE W_Sum = sumRows(M_temp) M_temp = M_temp[p][q] / W_Sum[p] // make output wave M_XY Make/D/O/N=(DimSize(M_Data,0), 2) M_XY // Do transformation to ternary coordinates; // Then use: AppendToGraph M_xy[][1] vs M_xy[][0] to add to ternary template M_XY[][0] = 0.5 * M_temp[p][2] + M_temp[p][1] M_XY[][1] = M_temp[p][2] * cos(30 * (pi/180)) end
Usage:
// make some data Make/D/O/N=(19,3) M_Data M_Data[0][0]= {62.9,51.5,60.1,63.5,44.6,56.8,43.3,74.1,0.3,1.2,52.4,66.1,63.3,54.1,73.3,0.3,0.3,89.7,88.5} M_Data[0][1]= {34.5,45.3,36.8,34.4,52.4,41.8,50.2,19.6,69.8,54.1,40.1,29.8,32.9,39.4,20.9,65.6,45.2,4.1,5.4} M_Data[0][2]= {2.6,3.2,3.1,2.1,3,1.4,2.3,1,15.1,14,1,1.4,1.6,2.4,0.8,15.9,30.5,4.8,4.2} // convert data ConvMatrix2Ternary(M_Data) // generate template MakeTernaryTemplate(crop=0.5) // append converted data AppendToGraph M_xy[][1] vs M_xy[][0]

Forum

Support
Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More
