
Finding the intersection point in a loop curve
I have two waves m and b. Each are scaled monotonically and equivalently by a third parameter x (from zero to unity in this case). I am looking for an efficient way to find the two x values where both m and b are equal.
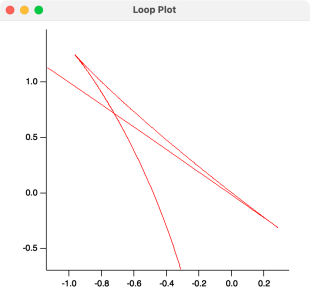
Imagine that a plot of m versus b. When both m and b are equal at one point along the line, the plot gives a loop as shown in the attached. I am looking for a way to find the intersection point of the loop as the (m,b,x) values.
Before I wrack my head with developing double for-loop iterations over all m with all b, am I missing a simpler way to find what I need?







If m and b are truly scaled equivalently, you're looking for a zero in m-b, right, so FindLevel should do it? Or am I missing something?
January 31, 2023 at 04:34 am - Permalink
@Tony -- I don't think it is this easy. I believe that just testing all algebraic combinations such as m + b, m - b, m/b, m*b for zeros or other constant values is not the answer.
The background might help. I have an equation for G = f(x) where G is a Gibb's energy of mixing a binary solution at mole fraction x. At the point where the binary solution separates into two phases (think oil and water), the plot of G versus x has a characteristic shape. See the plot attached. Focus only on the solid blue curve for G(x) (the dashed red is its derivative). The two points indicated by the cursors are the compositions at phase separation. The two points are contained on one line with the same slope m and intercept b.
I have extracted m(x) and b(x) along the entire curve G(x). The two points I want to find are x_lower and x_upper. I imagine I can brute force my way through two for-loops, one in the other, to test all (m,b) combinations to find the two x values where m_lower = m_upper and b_lower = b_upper.
When phase separation occurs, deconstruction from the G(x) curve generates a plot of m(x) versus b(x) that forms a loop. I am wondering if some "intersection" operation exists to find the (m,b) value at the closing point of the loop.
January 31, 2023 at 09:17 am - Permalink
Hi Jeremy,
Would an arc hull approach to the problem work? Finding the enclosing shape and then test for derivative changes signifying a change from the linear region to the curved region.
Andy
January 31, 2023 at 05:42 pm - Permalink
Rather than approaching this geometrically, have you thought about using Optimize to minimize the total free energy? You would need some sort of penalty function to satisfy mass balance constraints.
February 1, 2023 at 12:04 am - Permalink
Oh, you're calculating a solvus.
I take it you have functions for G(x) and G'(x), from these you can calculate the intercept b.
Unless you can accurately parameterize G vs b in a way that allows you to solve for an intercept, I think you need nested numerical solvers.
Here is what I would try:
EDIT: my proposed method was incorrect!
I wish I knew how CALPHAD or Thermocalc achieve this.
February 1, 2023 at 04:12 am - Permalink
Perhaps also relevant:
For calculating divariant binary phase loops, I use funcfit to fit a wave {0,0}.
The fit function returns for point 1 the difference in chemical potential of component one in phases A and B, and for point 2 the difference in chemical potential of component two in phases A and B.
To determine the phase A side of the loop, the fit coefficients are an intensive variable (P or T, one or the other is fixed) and the compositional variable (X1) for phase B, and the dependent variable is X1 for phase A. In this way I determine P(x) (or T(x)) that describes one side of the loop.
I use structure-based funcfit because there are a lot of thermodynamic parameters (end-member and mixing parameters) that need to be passed through the fit function to the Gibbs function. Keeping track of everything without structures would be challenging.
February 1, 2023 at 04:43 am - Permalink
Adapting the divariant loop method to a solvus calculation, maybe rewrite the fit function to return the difference in coefficients for the tangents at x1 and x2 (i.e. m2-m1 and b2-b1), and fit the {0,0} wave for x1 and x2 with 0<K0<1 and 0<K1<1 constraints.
February 1, 2023 at 05:35 am - Permalink
@Tony -- Thanks. Yes, I am finding the points on a two phase separation region. While I have an analytical form for the Delta G of mixing, I take the numerical derivative of the G to obtain mu.
I think I may have a clever way to find the intersection point without a for-loop. I will post back once I have tested it.
February 1, 2023 at 07:54 am - Permalink
Could you post the relevant equations for those of us who do not speak "phase separation"...
February 1, 2023 at 12:05 pm - Permalink
@AG -- I will post an experiment with the details once I have confirmed my method to find the loop intersection point.
February 1, 2023 at 12:51 pm - Permalink
My clever idea was not valid. I attach the experiment. Focus on the plot (m versus b). No loop is visible to report. Click on the non-ideal checkbox. A loop will appear in the (m versus b) graph. The loop intersection is the points 47 and 705 in the (m, b) waves. Notice where the points are on the (G, m) graph. The tie line that connects 47 and 705 have (nearly) the same slope and intercept. The goal is to find the two points on the common tie line.
I was mistaken. At the moment, I am using an analytical derivative equation to obtain mu(x). The analysis to find the loop intersection should not depend on having an analytical expression for mu = dG/dx.
February 1, 2023 at 01:46 pm - Permalink
Could you do it graphically? Sum up two black and white images (value 0 or 1) and look for the value 2.
February 2, 2023 at 04:17 am - Permalink
Well, your method works if you devise a way to establish the intersection point.
Here is my method using FuncFit:
EDIT: I added some comments to clarify how this works.
February 2, 2023 at 06:04 am - Permalink
@olelytken -- Perhaps. I think whatever image approach is used would have to include a dilation or blur. The (m,b) combinations are nearly the same but not perfectly the same.
@tony -- I will have to test your approach to understand it better. I would especially want to know how to change the approach to handle the case where Delta_{mix}G is defined numerically and mu is correspondingly obtain by numerical differentiation rather than analytically.
Many thanks to you both.
February 7, 2023 at 10:10 am - Permalink