Sorting columns of a 2D matrix

Share icon

Hi, 

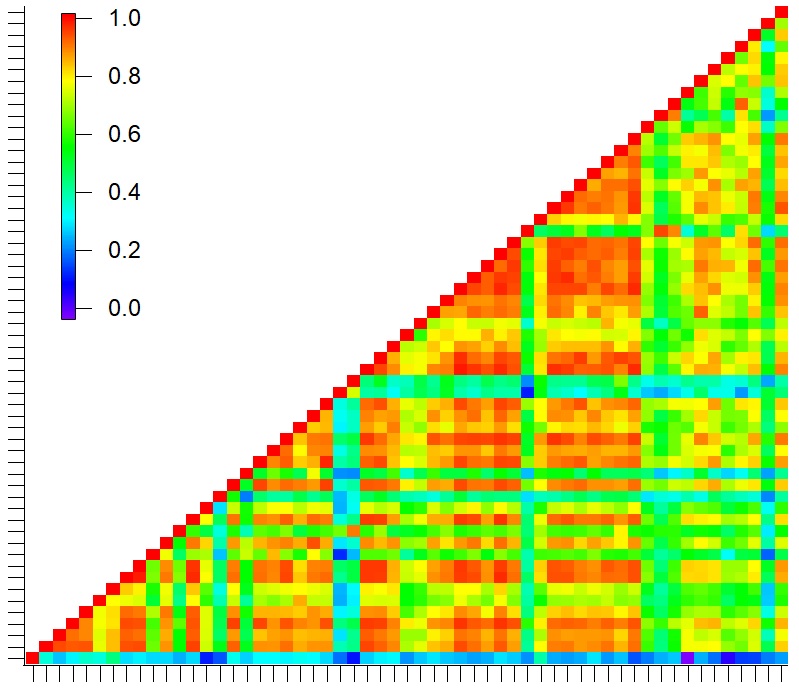
I am wondering whether there is a simple piece of code or library function to tackle this problem. Shown below is a correlation matrix. I want to sort the columns such that the columns get arranged in an increasing or decreasing order where order means the number of correlations. Each axis tick represents a compound- y and x-axis are the same list of compounds. So the sorted matrix will have reordering such that compounds with the highest number of good correlations will start from the right end of the axis moving toward the left. 

I'm not sure how I could achieve this. Kindly advise. 

Sincerely, 

Peeyush 

 

I am not completely sure how you define "the highest number of good correlations". Maybe you could plot them in the order of the correlation with the first column, or the order of the correlation with a specific column. Does "the highest number of good correlations" simply mean the sum of all values within that column?

December 19, 2021 at 12:02 pm - Permalink

Hi olelytken, 

Thanks for the question. In the figure, each pixel is a linear correlation value. So the column or row (any x or y axis tick in the image above) with the highest number of red pixels is the compound with the best correlations with other compounds in the matrix. Now I want to create segregation in the image where the compounds with the maximum number of red correlation pixels fall on one end and so on.. basically the image needs to be segregated just like the colorscale instead of how it is now where it's all mixed.

Sincerely, 

Peeyush

December 19, 2021 at 12:11 pm - Permalink

Maybe this will help. Here is the complete image of the correlation plot: Now I want the columns with the maximum number of red pixels to fall on the right of the x-axis and move toward the left segregated as the color scale. 

 

December 19, 2021 at 12:17 pm - Permalink

If I understand correctly, I think you could do

MatrixOp/O sumW = sumcols(myMatrix) // sum of all rows in columns
MatrixTranspose sumW // or do sumrows since this is equivalent in your example
Make/O/N=(DimSize(myMatrix,1)) indexW = p // make an index wave of row numbers
Sort sumW, sumW, indexW // sort your totals small to large. IndexW is now in the order you want
Make/O/N=(DimSize(myMatrix,0),DimSize(myMatrix,1)) newMatrix // make empty matrix
newMatrix[][] = myMatrix[p][indexW[q]] // assign the columns in the correct order

Caution: I have not tested this!!

December 19, 2021 at 02:23 pm - Permalink

@sjr51 -- I suspect that the summation method gives its own problems. Imagine columns are 10 steps high. One column has eight red pixels (value 10) and the rest blue (value 0). The neighboring column has nine orange pixels (value 9) and one blue (value 0). The first column sums to 80 and the second to 81. I believe the request is to have the first column rank higher than the second, while the summation method puts them in the opposite order.

December 19, 2021 at 04:36 pm - Permalink

Good point. So if good correlation means >0.5 (or whatever). He can do:

Duplicate/O myMatrix, myQMatrix // make a same sized matrix called myQMatrix
myQMatrix[][] = (myMatrix[p][q] > 0.5) ? 1 : 0 // if greater than 0.5 set to 1 otherwise 0
MatrixOp/O sumW = sumcols(myQMatrix) // sum of all rows in columns
MatrixTranspose sumW // or do sumrows since this is equivalent in your example
Make/O/N=(DimSize(myMatrix,1)) indexW = p // make an index wave of row numbers
Sort sumW, sumW, indexW // sort your totals small to large. IndexW is now in the order you want
Duplicate/O myMatrix, newQMatrix // make a same sized matrix called newMatrix
newMatrix[][] = myMatrix[p][indexW[q]] // assign the columns in the correct order

Now the summation tells us how many good correlations per column.

December 19, 2021 at 10:35 pm - Permalink