カーブフィッテイング

Igor Pro® には強力なカーブフィッティング機能が搭載されています。

• データを組み込みおよびユーザー定義のフィッティング関数にフィッテイングします。
• 線形回帰、多項式回帰、非線形回帰を行います。
• ユーザー定義のフィッティング関数において、フィッティング係数の数が事実上無制限です。
• 多変量カーブフィッティング（多重回帰）では、事実上無制限の数の独立変数を扱えます。
• データに対するカーブフィッティングは、フィッティングパラメーターに対する線形制約を伴います。
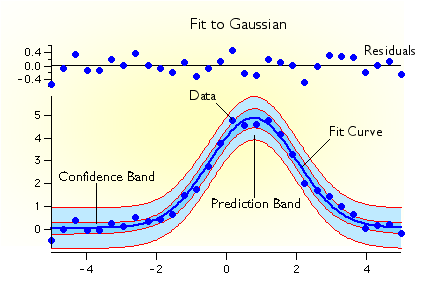
• モデルカーブ、カーブフィッティング残差、信頼帯、予測帯を自動的に計算します。これらのカーブはデータグラフに自動的に追加できます。
• オプションでフィッティング係数の信頼区間を自動的に計算します。
• 任意のフィッティング係数の値を設定し、保持します。
• 重み付けデータフィッティングを行います。
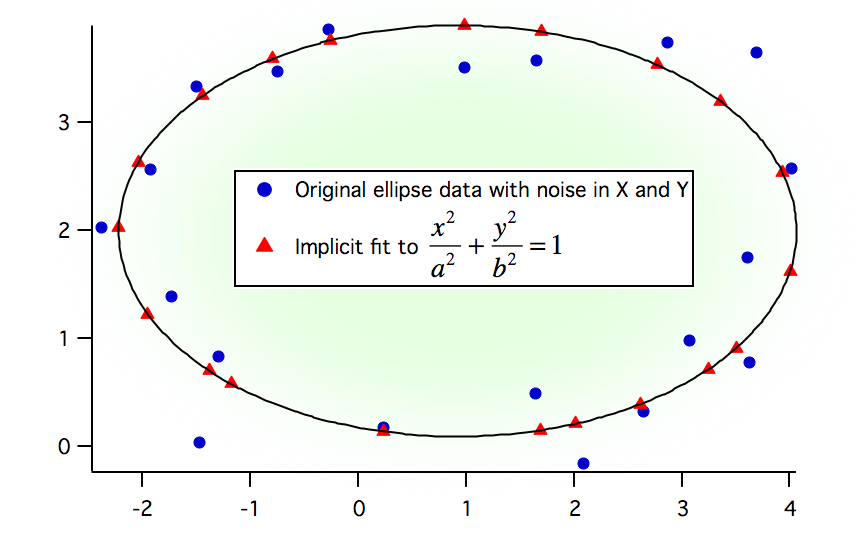
• 変数誤差フィッティング（X と Y の両方に測定誤差がある場合）を行います。
• フィッティング関数が f(x,y)=0 の形をとる場合、暗黙的フィッティングを行います。
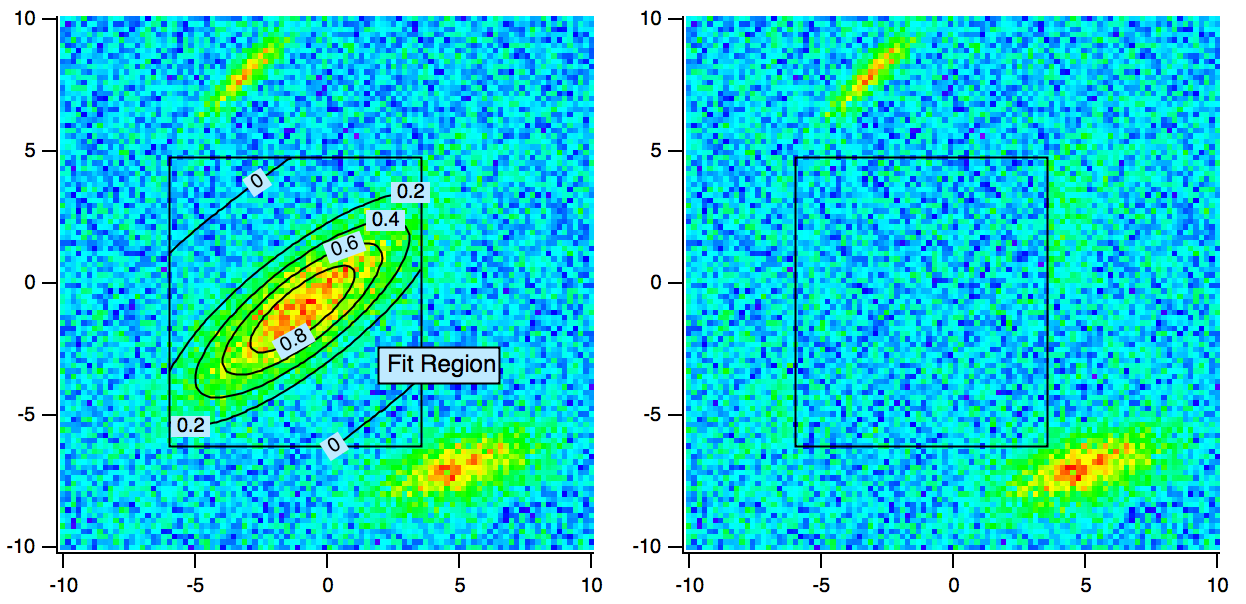
• データのサブセットに対するカーブフィッティングを行います。
• 組み込み関数への簡易なフィッティングは、１回のメニュー選択で実行できます。
• フィッティング関数の和にフィッティングします。
• 反復フィッティング中に自動グラフ更新でフィッティングの進捗を追跡します。
• 反復的または特殊なカーブフィッティング作業向けに完全にプログラム可能です。
• ユーザー定義のフィッティングは複数のプロセッサを活用します。
• 複数プロセッサを用いた同時フィッティングのためのプログラマ向けのサポートがあります。

Igor Pro の基本的なカーブフィッティング機能に基づいて構築されたパッケージは、機能を追加します。

• Global Analysis
• Peak Analysis

カーブフィッティングの概要

カーブフィッティングの目的は、データに適合する数学的モデルを見つけることです。特定の形の関数を選択する理論的根拠があるものと仮定します。カーブフィッティングは、その関数をデータに可能な限り一致させるための具体的な係数（パラメーター）を求めます。数千もの関数の中からデータに合うものを探すためにカーブフィッティングを使おうとする人もいます。Igor Pro はこの目的のために設計されたものではありません。

カーブフィッティングでは、生データと未知の係数を持つ関数があります。関数が生データに可能な限り一致するように、係数の値を見つけるのが目的です。係数の最適な値は、カイ二乗値を最小化するものである。カイ二乗は次のように定義されます。

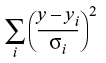
ここで、y は特定の点に対する推定値（モデル値）、y_i はその点の測定データ値、σ_i は y_i の標準偏差の推定値です。

最も単純なケースは、データを直線にフィッテイングさせる場合です：y = ax + b、これは「線形回帰」とも呼ばれます。データが直線上に収まるはずだと理論的に考える理由があるとします。データに最もよく合う係数 a と b を求めるのが目的です。直線や多項式関数へのカーブフィッティングでは、最適係数を１ステップで見つけることができます。Igor Pro は特異値分解アルゴリズムを使います。

反復データフィッティング（非線形最小二乗法／非線形回帰）

その他の組み込みデータフィッティング関数およびユーザー定義関数については、操作は反復的である必要があります。Igor Pro は未知の係数に対して様々な値を試します。試行ごとに、カイ二乗を計算し、カイ二乗の最小値をもたらす係数値を検索します。

初期推定値

Igor Pro は、非線形最小二乗データフィッティングでは、カイ二乗の最小値を検索するために Levenberg-Marquardt アルゴリズムを使います。カイ二乗は多次元誤差空間でサーフェスを定義します。検索プロセスでは、係数値の初期推定値から開始します。初期推定値から開始して、カイ二乗サーフェス上の開始点から下り坂を進むことで最小値を検索します。

カイ二乗サーフェスで最も深い谷を見つけるのが目的です。これは、サーフェス上のポイントであり、そのポイントでは、フィッティング関数の係数値が、最小二乗の意味で、実験データとフィッティングデータ（モデル）との差を最小化します。いくつかのカーブフィッティング関数には、谷を１つだけ持つかもしれません。この場合、谷底が見つかった時点で最良のフィッティングが得られたことになります。しかし、フィッティング関数によっては複数の谷（周囲の値よりもフィッティング精度が高い場所）を持つ場合があり、それが最良のフィッティングとは限らないこともあります。Igor Pro が谷底を見つけた場合、表面の他の場所にさらに深い谷がある可能性があっても、フィッティングは完了したと判断します。Igor Pro が最初にどの谷を見つけるかは、初期推定値によって異なります。

組み込みのカーブフィッティング関数では、Igor Pro に初期推定値を自動的に設定させることができます。これで満足のいく結果が得られない場合は、手動での推定を試みることができます。ユーザー定義関数へのデータフィッティングでは、手動での推定値を指定する必要があります。

複数のピークが重なっている可能性があるデータを持っている場合、マルチピークパッケージがデータを自動的に解析し、データフィッティング前に初期推定値を生成します。

その他のデータフィッティングアルゴリズム

時々、ユーザーから Levenberg-Marquardt 法の代替として、シミュレーテッドアニーリングなどの他のデータフィッティングアルゴリズムについて問い合わせがあります。しかし、これまでのところ、Levenberg-Marquardt 法よりも優れた結果を出すアルゴリズムは確認されていません。 そのようなアルゴリズムやデータセットをご存知でしたら、お知らせください。

シミュレーテッドアニーリングには、グローバルミニマム（カイ二乗分布の表面における最も深い谷）を発見できる可能性があるという魅力があります。これは非常に時間がかかり、決して保証されるものではありません。シミュレーテッドアニーリングフィッターを構築するには、Igorの関数最適化操作のシミュレーテッドアニーリングオプションを利用できます。その後、標準フィッターを用いて結果を「磨き上げ」、誤差推定値を提供します。