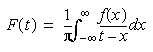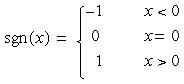ヒルベルト変換

関数 f(x) のヒルベルト変換は次のように定義されます。

理論的には、積分はコーシーの主値として評価されます。計算上では、ヒルベルト変換を畳み込みとして記述できます。

フーリエ変換の畳み込み定理により、これは関数 f(x) の変換と -i*sgn(x) の積として評価できます。ここで：

ヒルベルト変換は、入力信号の全周波数成分の位相を単に -π/2 ラジアンだけシフトするフィルターと見なすことができます。

「解析的」（複素時間）信号 Y(t) は、実数値入力信号 y(t) から構築できます。

• Y(t) = y(t) + j h(t)

ここで、

• Y(t) は y(t) およびそのヒルベルト変換から構成される解析信号です
• y(t) は入力信号です
• h(t) は入力信号のヒルベルト変換です

実部と虚部は極座標で次のように表すことができます。

• Y(t) = A(t) exp[jψ(t)]

ここで、

• A(t) は解析信号の「エンベロープ」または振幅です
• ψ は解析信号の位相です（ψ の導関数は「瞬間周波数」と呼ばれます）

次の Igor Pro® コマンドは、ヒルベルト変換操作を用いて信号の「エンベロープ」を計算します。

	HilbertTransform inputSignal	// creates W_Hilbert
	Rename W_Hilbert, envelope
	envelope= real(r2polar(cmplx(inputSignal[p], envelope[p])))

定数のヒルベルト変換はゼロであることに注意してください。多次元でヒルベルト変換を計算し、そのうちの１つの次元が変化しない（定数である）場合、変換はゼロとなります（少なくとも数値的にはゼロに近い値となります）。

Igor Pro の HilbertTransform コマンドは、１～３次元の実数または複素数（単精度または倍精度）データのヒルベルト変換を計算します。

参考文献

• Bracewell, R., The Fourier Transform and Its Applications, McGraw-Hill, 1965.
• Feldman, M., "Non-linear system vibration analysis using Hilbert Transform - I. Free Vibration Analysis Method 'FREEVIB'", Mechanical Systems and Signal Processing (1994) 8(2), 119-127.