畳み込みと相関

畳み込みを使って、入力信号に対する線形システムの応答を計算できます。線形システムはそのインパルス応答によって定義されます。入力信号とインパルス応答の畳み込みが、出力信号の応答となります。畳み込みはまた、周波数領域におけるフィルタリングの時間領域における対応物でもあります。

Igor Pro® は Convolve コマンドで一般的な畳み込みを実装します（平滑化も畳み込みの一種です）。Convolve コマンドを使うには、Analysis メニューから Convolve を選択します。

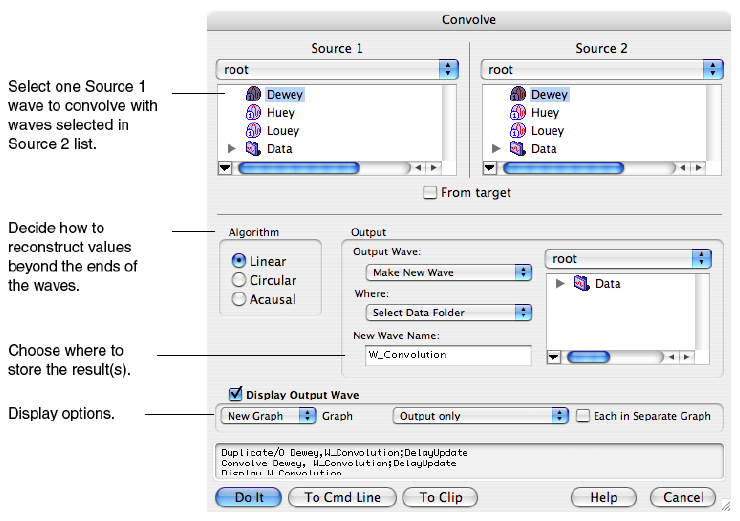
組み込みの Convolve コマンドは、「ソース」および「宛先」という２つのウェーブの畳み込みを計算し、結果で宛先ウェーブを上書きします。このコマンドは、１つのソースウェーブを複数の宛先ウェーブと畳み込むこともできます（それぞれのケースで、対応する宛先ウェーブを結果で上書きします）。Convolve ダイアログでは、２番目のウェーブを新しい宛先ウェーブに事前に複製することで、より柔軟に対応できます。

ソースウェーブが実数値の場合、各宛先ウェーブも実数値でなければならず、ソースウェーブが複素数の場合、各宛先ウェーブも複素数でなければなりません。倍精度と単精度ウェーブは自由に混在可能であり、計算は高い精度で行われます。

畳み込みは、畳み込み対象ポイントの直前と直後の隣接ポイントを組み合わせますが、ウェーブの端では十分な隣接ポイントが存在しません。これはあらゆる畳み込み操作における一般的な問題であり、平滑化操作では End Effect ポップアップを使って対処方法を決定します。Convolve ダイアログの Algorithm グループには、これらの欠落点を処理するための３つのアルゴリズムが用意されています。

Linear アルゴリズムは、Smooth コマンドのゼロ端点効果法に類似しており、欠落した隣接ポイントの値はゼロで置き換えられます。

Circular アルゴリズムはラップエンド効果法に類似しており、このアルゴリズムはデータが無限に繰り返すと想定される場合に適しています。

非因果アルゴリズムは Linear の特殊なケースであり、Linear が導入する時間遅延を排除します。

選択したアルゴリズムに応じて、宛先ウェーブのポイント数は、ソースウェーブのポイント数から 1 を引いた数だけ増加する場合があります。線形および非因果畳み込みの場合、宛先ウェーブはまず、ソースウェーブのポイント数より 1 少ない数だけゼロパディングされます。これにより、循環畳み込みで発生する「ラップアラウンド」効果を防ぎます。ゼロパディングされたポイントは、非因果畳み込み後は除去され、線形畳み込み後は保持されます。

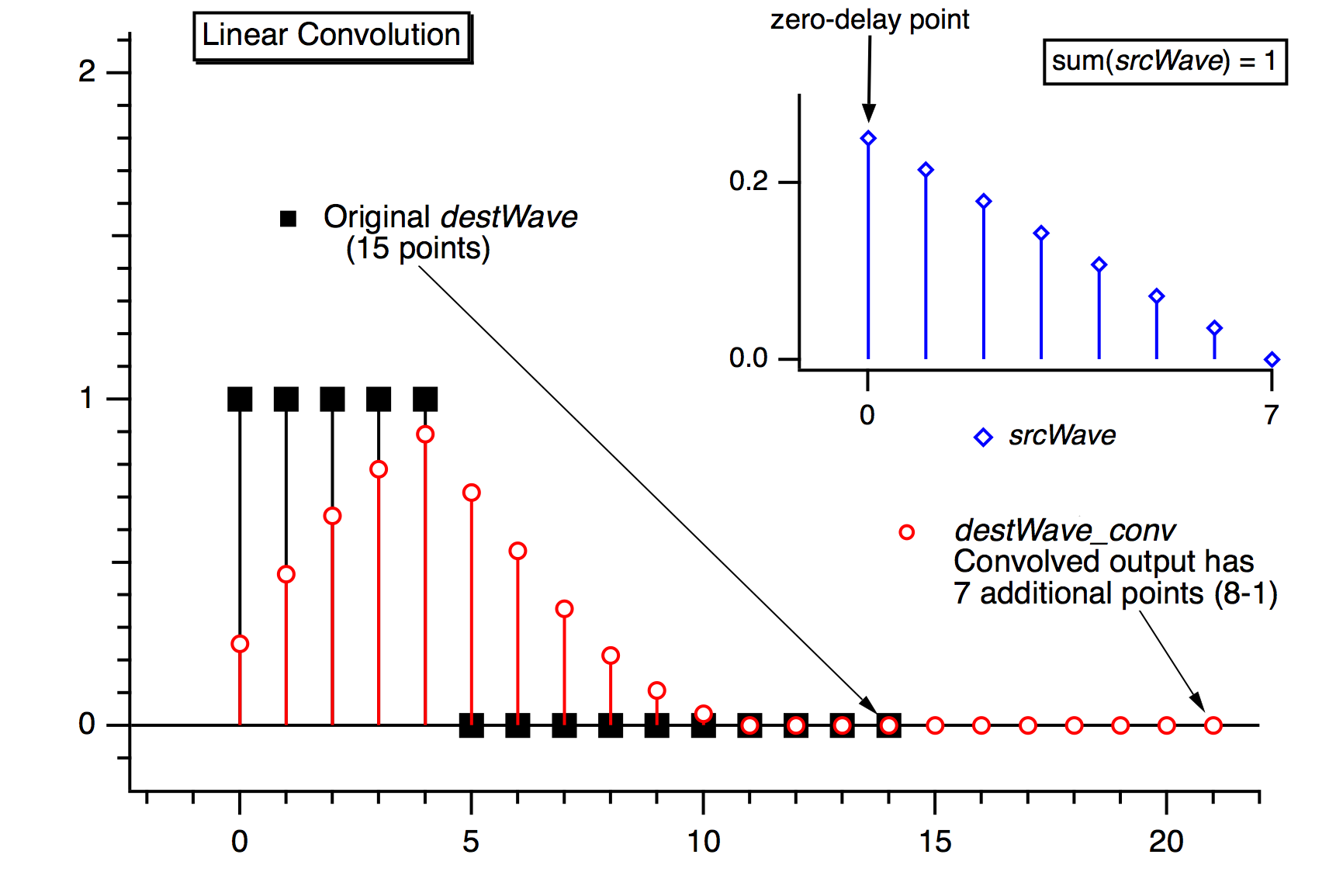
ソースウェーブにインパルス応答（またはフィルター係数）が含まれる場合、srcWave の最初のポイントが遅延なし（t=0）に対応するときは線形畳み込みを使います。

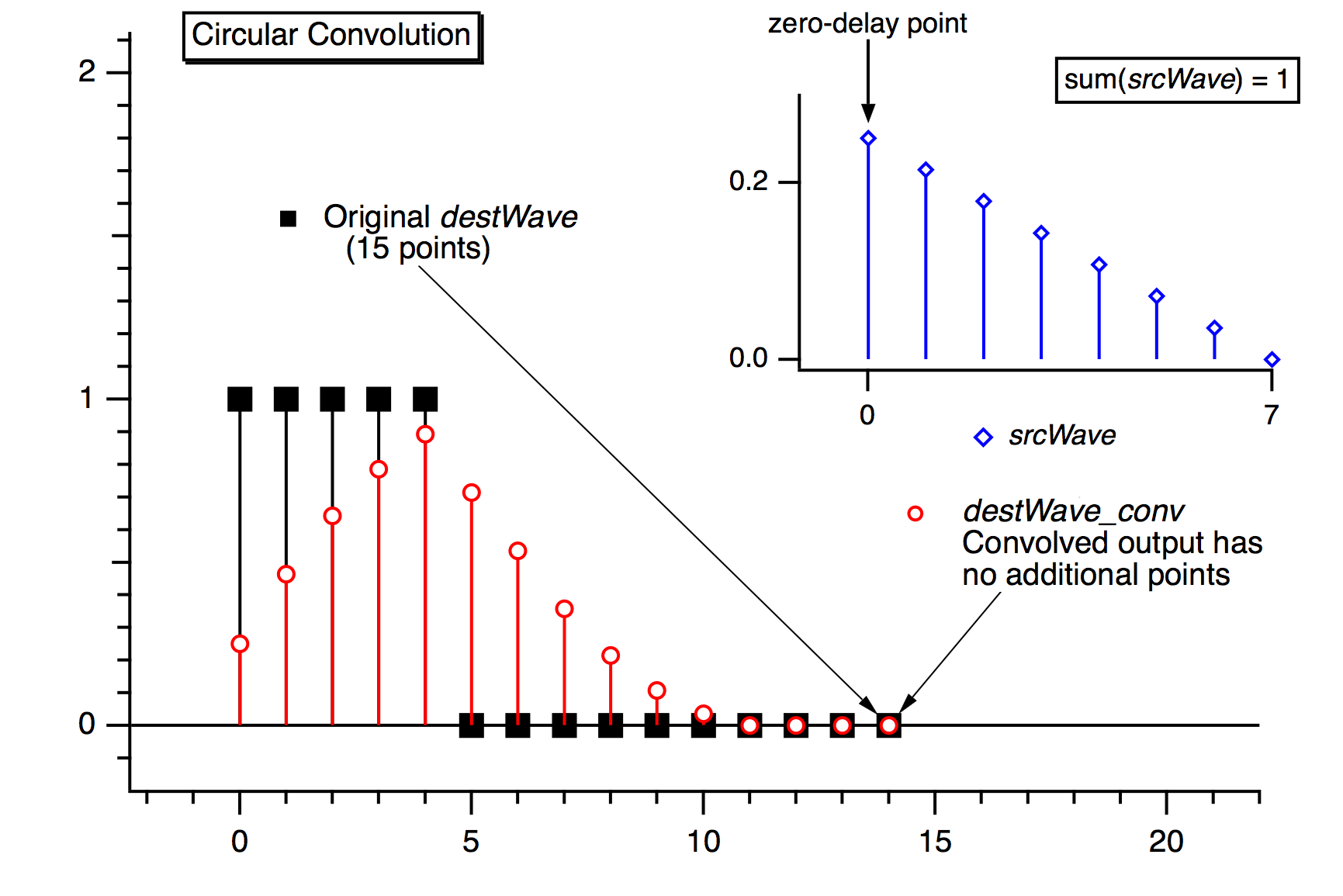
ソースウェーブと宛先ウェーブのデータが無限に繰り返し（または「終わりから始まりへ折り返す」）とみなされる場合には Circular 畳み込みを使います。これはゼロパディングが不要であることを意味します。

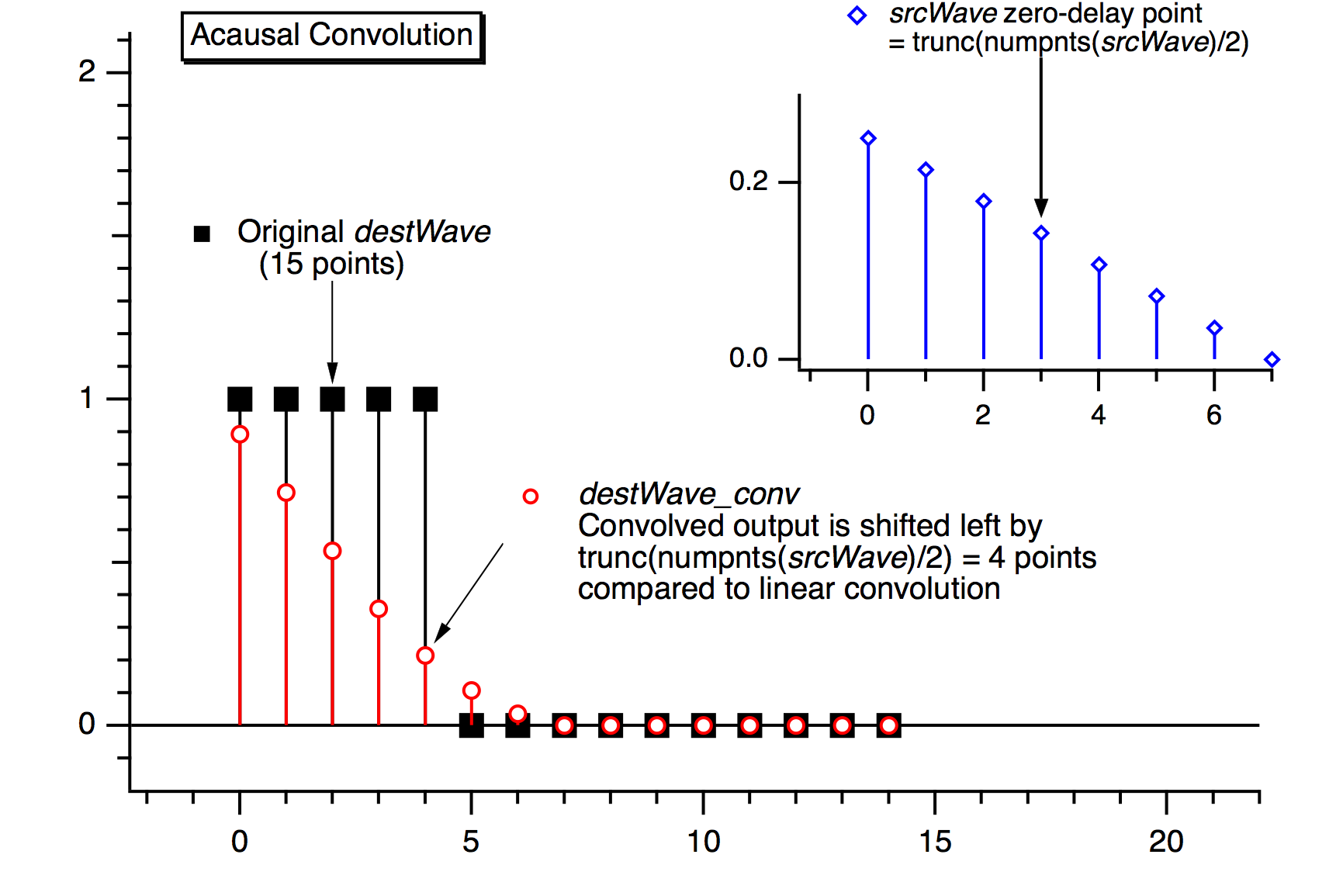
ソースウェーブにインパルス応答が含まれる場合、ソースウェーブの中間点が遅延なし（t=0）に対応するときは、非因果畳み込みを使います。

相関

相関を使って、２つのデータセットの類似性を比較することができます。相関は、互いにシフトされた２つの入力信号の類似性の尺度を計算します。相関の結果は、２つの信号が最も一致する時点で最大値に達します。２つの信号が同一の場合、この最大値は t=0（遅延なし）で到達します。２つの信号が類似した形状を持つが、一方が時間的に遅延し、ノイズが加わっている可能性がある場合、相関はその遅延を測定する優れた方法です。

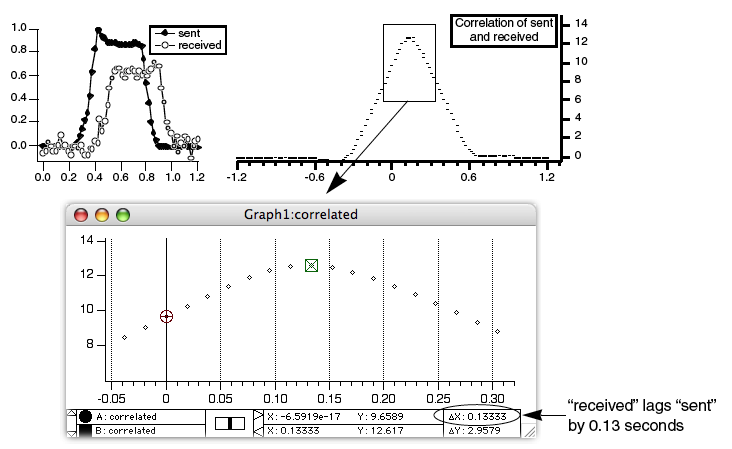
Igor Pro は Correlate コマンドで相関を実装します。Analysis メニューの Correlate ダイアログは Convolve ダイアログと同様に動作します。ソースウェーブは宛先ウェーブでもよく、その場合、宛先ウェーブにはそのウェーブの「自己相関」が含まれます。ソースと宛先が異なる場合、「相互相関」と呼ばれます。

異なるタイプのソースウェーブと宛先ウェーブを組み合わせる時の考慮事項は、畳み込みと同様に相関にも適用されます。相関もまた端部効果に対処する必要があり、これらは Circular 相関と Linear 相関アルゴリズムの選択によって処理されます。

ピアソンの r 相関

Igor Pro の StatsLinearCorrelationTest コマンドを使うと、２つのデータセットの相関について１つの相関係数（ピアソンの r と呼ばれる）を計算できます。ピアソンの線形相関係数 r は次の式で与えられます：

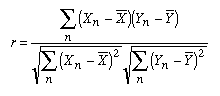
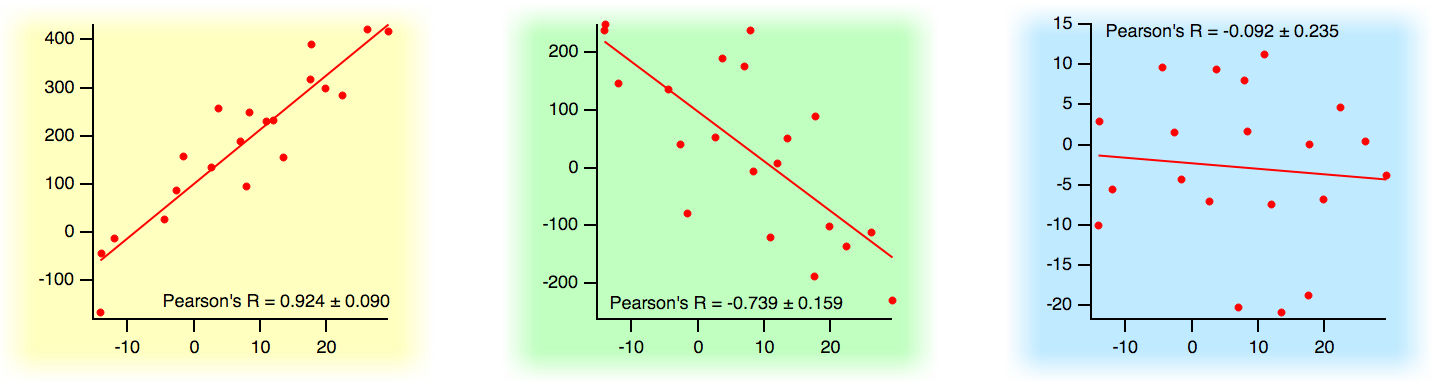
ピアソンの相関係数 r は、２つのデータセット間の直線関係の程度を反映します。その値は -1 から +1 の間です。+1 の値は、２つのデータセット間に完全な正の直線関係があることを意味します。-1 の値は完全な負の直線関係があることを意味し、0 の値はデータセット間にまったく直線関係がないことを意味します。実際には中間値となることが多いです。以下の３つのグラフは、共通の基準データセットに対してプロットされた３つの異なるデータセットを示しています。これら３つのデータセットは、基準データセットとの相関の度合いがそれぞれ異なります。（参考として直線近似も示されていますが、ピアソンの r は直線フィッティングの傾きを示していません。）

参考文献

• Press, William H. [et. al.], "Fourier and Spectral Applications", sec. 13, Numerical Recipes in C, 2nd ed., Cambridge University Press, 1992.
• Press, William H. [et. al.], "Linear Correlation", sec. 14.5, Numerical Recipes in C, 2nd ed., Cambridge University Press, 1992.