変数誤差によるフィッティング

モデルをデータにフィッティングさせる時、通常はすべての誤差が従属変数に存在し、独立変数は完全に既知である（つまり、X は完全に設定され、Y は誤差を伴って測定される）と仮定されます。この仮定は往々にして真実に近く、従属変数の誤差が独立変数の誤差よりもはるかに大きい限り、カーブフィッティングに大きな差異をもたらすことは通常ありません。

誤差が平均ゼロで分散が一定な正規分布に従い、かつモデルが正確である場合、標準最小二乗法によるフィッティングは最尤解を与えます。

しかし、場合によっては、従属変数と独立変数の両方に同程度の誤差が生じることもあります。この状況は、変数誤差、測定誤差モデル、ランダム回帰モデルなど、さまざまな名前で呼ばれています。従属変数と独立変数で類似した誤差が生じうるモデルの一例として、物体の軌跡を表面に沿ってフィッティングさせる場合が挙げられます。関与する変数は、物体の位置に関する直交座標の測定値（様々な時点における）となります。双方とも空間的測定を伴うため、おそらく測定誤差は類似しています。

標準最小二乗法や通常の最小二乗法を用いてこのようなデータをフィッティングすると、解にバイアスが生じる可能性があります。この問題を解決するため、直交距離回帰（ODR）を提供します。従属変数における二乗誤差の総和を最小化するのではなく、ODR はモデル係数と独立変数の値への調整の両方を調整することで、データからフィッティングカーブへの直交距離を最小化します。これは「総最小二乗法」とも呼ばれることがあります。

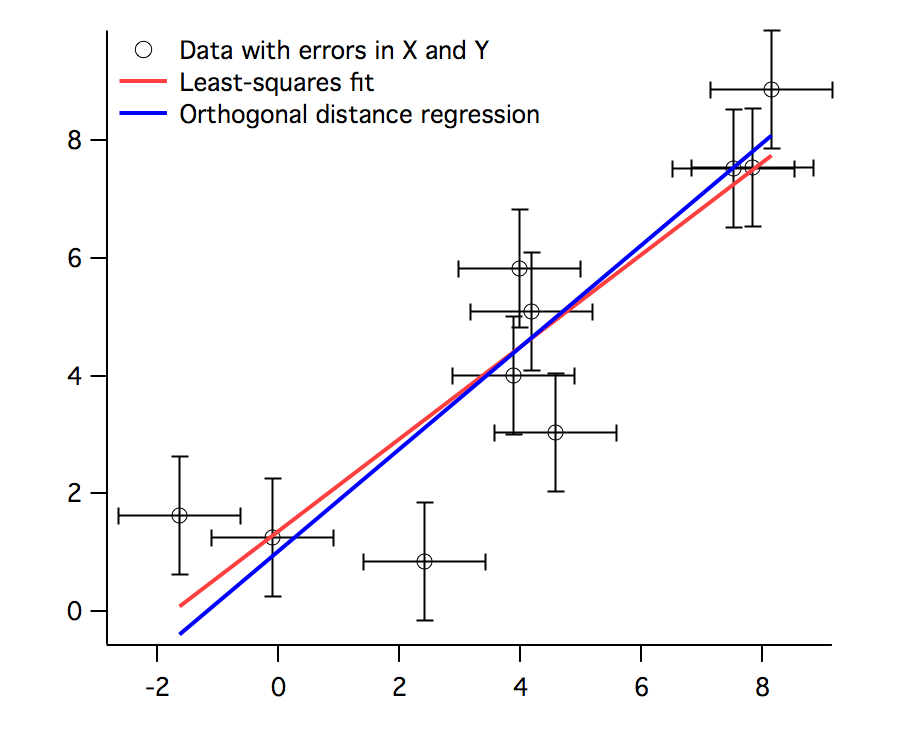
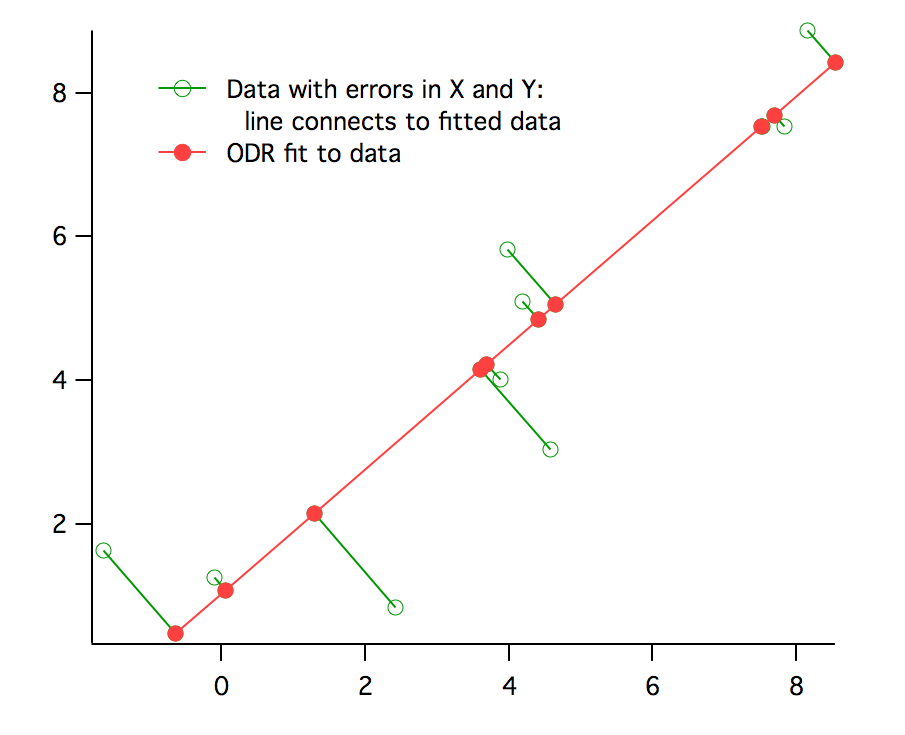
ODR カーブフィッティングには、Igor Pro® は無料で利用可能な ODRPACK95 を使います。詳細については、以下の論文を参照してください：

Boggs, P.T., R.H. Byrd, and R.B. Schnabel, A Stable and Efficient Algorithm for Nonlinear Orthogonal Distance Regression, SIAM Journal of Scientific and Statistical Computing, 8, 1052-1078, 1987.

Boggs, P.T., R.H. Byrd, J.R. Donaldson, and R.B. Schnabel, Algorithm 676 - ODRPACK: Software for Weighted Orthogonal Distance Regression, ACM Transactions on Mathematical Software, 15, 348-364, 1989

Boggs, P.T., J.R. Donaldson, R.B. Schnabel and C.H. Spiegelman, A Computational Examination of Orthogonal Distance Regression, Journal of Econometrics, 38, 169-201, 1988.