
信号処理
信号処理とは、分析や強化を目的として取得した時系列データを修正する技術と科学です。例としてはスペクトル解析(高速フーリエ変換やその他の変換を用いた)や、デジタルフィルタリングによる取得データの強化などが挙げられます。
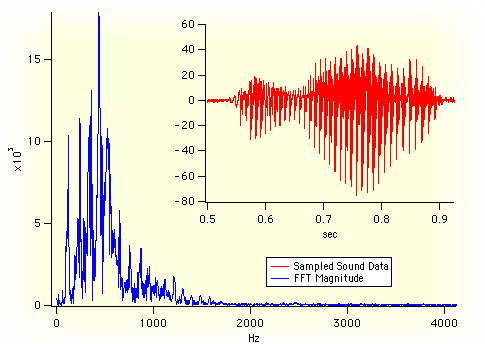
Igor Pro® は、長時間の時系列(または「ウェーブフォーム」)データの強力なサポートを備えていること、そして多くの組み込みの信号処理コマンドがシンプルなダイアログを通じて容易に使用できることから、信号処理に最適です。
さらに、Igor Pro のプログラミング言語は、あらゆる種類のカスタム信号処理アルゴリズムの実装を容易にします。これは、Igor Pro のフーリエ変換(およびその他の変換)の強力な機能によって大きく支援されています。
フーリエ変換
Igor Pro は高速フーリエ変換(FFT)アルゴリズムを用いて離散フーリエ変換(DFT)を計算します。FFT は信号の振幅と位相を単純に特徴付けるために使用できるほか、他の演算と組み合わせて畳み込みや相関といったより複雑な計算を実行するためにも使用できます。
スペクトル・ウインドウ処理
FFT の計算は、入力データが繰り返すことを前提としています。データの最初と最後の値が異なる場合、この点は重要です。不連続性が FFT によって計算されるスペクトルに異常をもたらします。「ウインドウ処理」は、データの端を平滑化してこうした異常を除去します。
パワースペクトル
パワースペクトルは「どの周波数帯域に信号の電力が集中しているか」という問いに答えます。その答えは、周波数関数としての電力値の分布という形で示されます。ここで「電力」とは信号の二乗の平均値とみなされます。周波数領域では、これは FFT の振幅の二乗に相当します。
パワースペクトルは信号全体に対して一括してコンピューターで計算することもできます(「スペクトログラム」)。あるいは時間信号の区間のスペクトログラムを平均化して「パワースペクトル密度」を形成することもできます。
ヒルベルト(Hilbert)変換
ヒルベルト変換は、入力信号に対して 90 度「位相がずれた」時間領域信号を計算します。一次元的な応用例には、変調信号のエンベロープの計算や、減衰が緩やかな線形・非線形システムで頻繁に遭遇する指数関数的に減衰する正弦波の減衰率測定が含まれます。
時間周波数解析
信号のフーリエスペクトル(またはパワースペクトル)を計算すると、フーリエ変換に含まれる位相情報はすべて失われます。信号に含まれる周波数は特定できますが、それらの周波数が信号内のいつ現れるかはわかりません。例えば、次の信号を考えてみます:
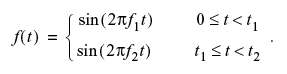
2つの周波数 f1 と f2 を入れ替えても、f(t) のスペクトル表現は本質的に変わりません:
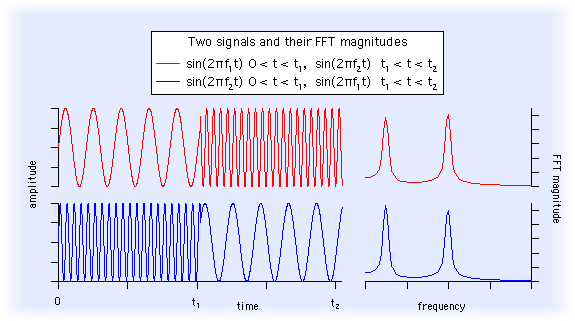
明らかにフーリエスペクトルは、スペクトルが時間とともに変動する信号の分析ツールとしては最適ではありません。
この問題に対する 1 つの解決策は、いわゆる「短時間フーリエ変換」(または「ソノグラム」)であり、これは、スライディング時間ウィンドウを使ってフーリエスペクトルを計算することができます。ウィンドウの幅を調整することで、結果のスペクトルの時間分解能を決定することができます。
その他の代替ツールとしては、ウィグナー変換、連続ウェーブレット変換 (CWT)、離散ウェーブレット変換 (DWT) などがあります。
畳み込みと相関
畳み込みを使って、入力信号に対する線形システムの応答を計算できます。線形システムはそのインパルス応答によって定義されます。入力信号とインパルス応答の畳み込みが、出力信号の応答となります。デジタルフィルタリングは、信号と畳み込み演算を行うことで望む結果(ローパスフィルターまたはハイパスフィルター)を達成する線形システムのインパルス応答を定義することで実現されます。
相関アルゴリズムは数学的には畳み込みと非常に似ていますが、異なる目的で使われます。最も頻繁に用いられるのは、2つの信号が「一致する」、あるいは「最も類似する」時間遅延を特定するためです。
スムージング
スムージング(平滑化)は短期的な変動、すなわち「ノイズ」を除去し、データの重要な本質的な形を明らかにします。
最も単純なスムージング手法は「移動平均」で、各データ値を隣接する値の平均値で置き換えるだけです(この種のスムージングは「スライディングスムージング」「ボックススムージング」「ボックスカースムージング」とも呼ばれます)。
Igor Pro のスムージング操作は、ボックススムージング、「二項」(ガウス)スムージング、Savitzky-Golay(多項式)スムージングを実行します。異なるスムージングアルゴリズムは、隣接する値に異なる重みまたは「係数」を乗算して平滑化された値を計算する加重平均を算出します。
デジタルフィルター
データが既にデジタル化されている場合、デジタルフィルターは自然な手段です。データにデジタルフィルタリングを適用する理由には次のようなものがあります:
- 不要な信号成分(ノイズ)の除去
- 必要な信号成分の増強
- 特定信号の存在の検出
- 線形システムのシミュレーション(入力信号とシステムの「伝達関数」から出力信号を計算)
デジタルフィルターは一般的に、有限インパルス応答(FIR)フィルターと無限インパルス応答(IIR)フィルターの2種類に分類されます。
Igor Pro は主に時間領域畳み込みを用いてデジタルフィルタリングを実装しており、FilterFIR、FilterIIR、Smooth コマンドを使います。
Igor 6 以降では、Analysis→Filter メニュー項目が追加され、フィルター設計と適用ダイアログが開きます:
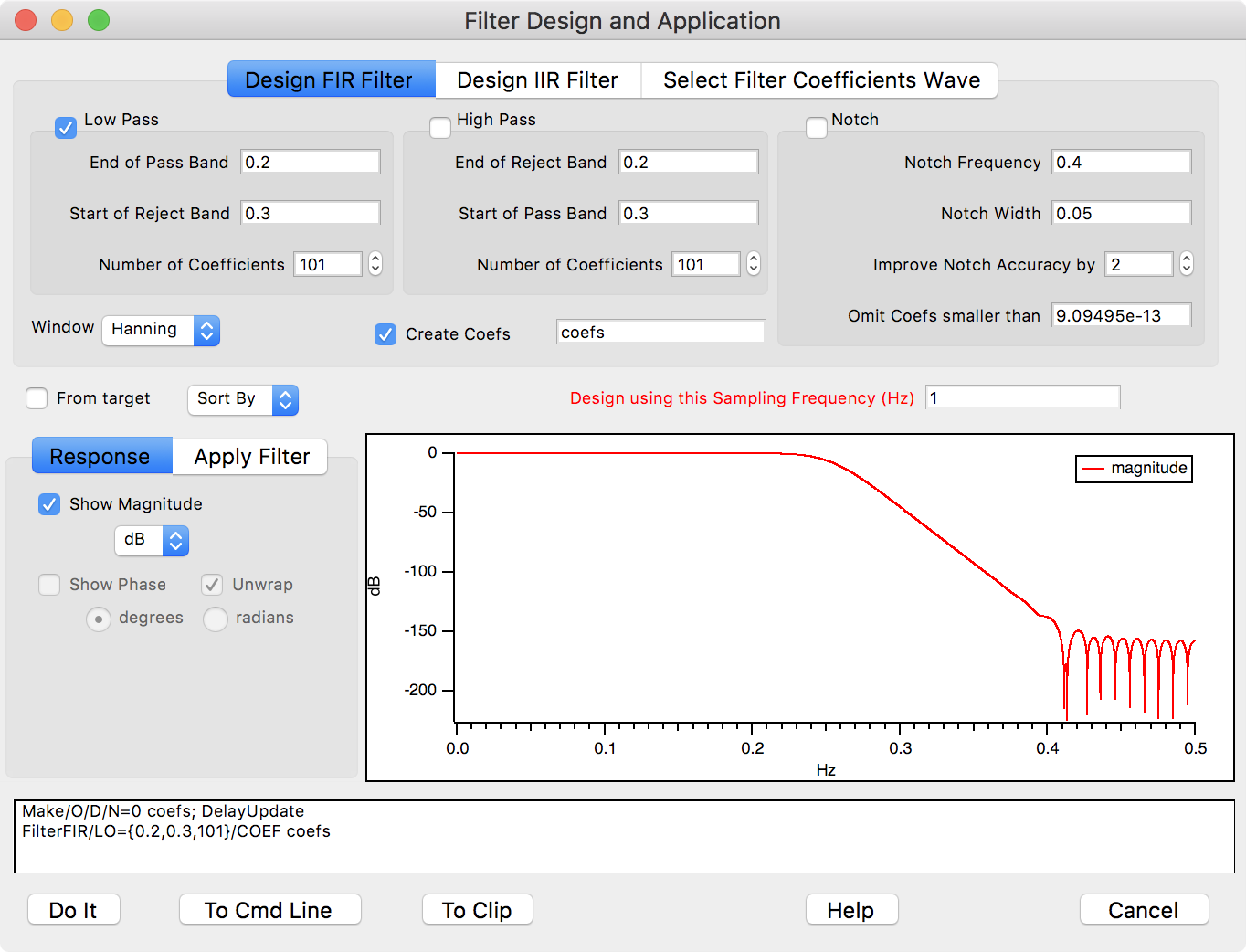
FIR フィルターと IIR フィルターを設計する別の方法として、Igor Filter Design Laboratory があります。
レベル検出
レベル検出とは、データが特定の Y 値を通過または到達する X 座標を特定するプロセスです。これは「逆補間」と呼ばれることもあります。別の言い方をすれば、レベル検出は「与えられた Y レベルに対応する X 値は何か?」という問いに答えるものです。
Igor Pro はその質問に対して2種類の回答を提供します。1つの回答は、Y データが一意の Y 値のリストであり、単調増加または単調減少すると仮定するものです。
もう1つの回答は、取得データの場合のように Y データが不規則に変動することを前提とします。この場合、Y レベルを横切る X 値が複数存在する可能性があります。この重要な例として、エッジとパルス統計が挙げられます。
関連はありますが異なる問題として、「関数 y = f(x) が与えられたとき、y が 0(または他の値)となる x を求めよ」という問題があります。この問題は、FindRoots コマンドによって解決されます。
ピークを検出するには、ピーク分析を参照してください。
Igor Pro の信号処理コマンド
| area | areaXY | BinarySearch |
| BinarySearchInterp | Convolve | Correlate |
| CWT | Differentiate | DSPDetrend |
| DSPPeriodogram | DWT | EdgeStats |
| faverage | faverageXY | FFT |
| FindLevel | FindLevels | Hanning |
| HilbertTransform | IFFT | ImageWindow |
| Integrate | Interp2D | Interp3d |
| interp | PCA | PulseStats |
| Rotate | Smooth | SmoothCustom |
| Unwrap | WignerTransform |

Forum

Support

Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More