平滑化

平滑化は短期的な変動、すなわち「ノイズ」を除去し、データの重要な本質的な形を明らかにします。

Igor Pro® のスムージング操作は、ボックス、二項、および Savitzky-Golay 平滑化を実行します。異なる平滑化アルゴリズムは、入力データを異なる係数で畳み込みます。

平滑化は一種のローパスフィルターです。平滑化のタイプと平滑化の程度によって、フィルターの周波数応答が変化します。

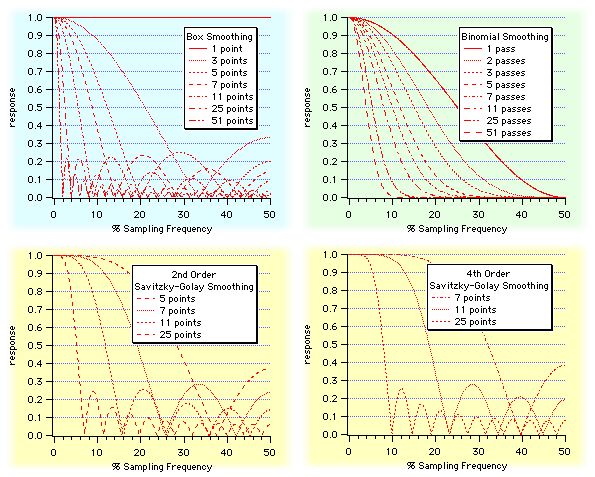
移動平均（別名「ボックス平滑化」）

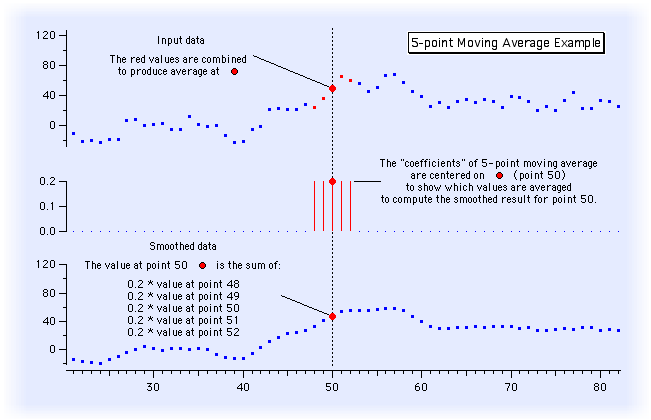
平滑化の最も単純な形式は「移動平均」で、これは単に各データ値を隣接する値の平均値で置き換えるものです。データのずれを避けるためには、平均を計算する位置の前後で同じ数の値を平均化するのが最善です。数式で表すと、移動平均は次のように計算されます：

この種の平滑化は、「スライディング平均」、「ボックス平滑化」、あるいは「ボックスカー平滑化」とも呼ばれます。これは、入力データを 2*M+1 個の値すべてが 1/(2*M+1) である箱型のパルスで畳み込みすることで実装できます。これらの値を「平滑化カーネル」の「係数」と呼びます。

二項平滑化

二項平滑化はガウスフィルターです。平滑化パラメーターに等しいレベルでパスカルの三角形から導出された正規化係数でデータを畳み込みます。このアルゴリズムは Marchand and Marmet（1983）の論文から導出されています。

Savitzky-Golay 平滑化

Savitzky-Golay 平滑化は、化学分野で広く用いられている事前計算済み係数の異なるセットを使います。これは最小二乗多項式平滑化の一種です。平滑化の程度は、多項式の次数と、各平滑化出力値の計算に使われるポイント数の２つのパラメーターによってコントロールされます。

参考文献

• Marchand, P., and L. Marmet, Binomial smoothing filter: A way to avoid some pitfalls of least square polynomial smoothing, Rev. Sci. Instrum., 54, 1034-41, 1983.
• Savitzky, A., and M.J.E. Golay, Smoothing and differentiation of data by simplified least squares procedures, Analytical Chemistry, 36, 1627-1639, 1964.