フーリエ変換

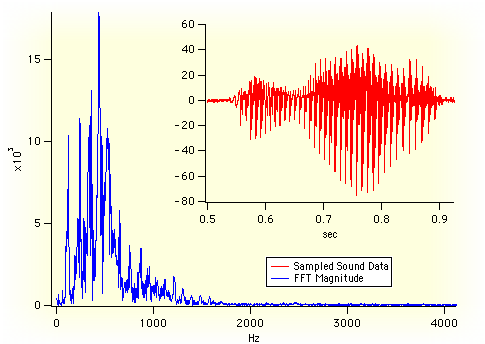
• フーリエ変換は、線形システムの特性評価や連続ウェーブフォームを構成する周波数成分の同定に長年用いられてきました。しかし、ウェーブフォームがサンプリングされた場合、あるいはシステムをデジタルコンピューター上で解析する場合、理解し使うべきは有限で離散的なフーリエ変換（DFT）です。連続フーリエ変換（CFT）の性質の大半は保持されているものの、DFT が有限区間で定義されるサンプリングウェーブフォームに対して作用しなければならないという制約から、いくつかの相違点が生じます。


• 高速フーリエ変換（FFT）は、単に DFT を計算するための効率的な手法です [1]

フーリエ変換は、時間領域のデータを周波数領域で表現し、その逆も行う能力を持ち、多くの応用があります。最も頻繁な応用の一つは、等間隔の時間間隔でサンプリングされたデータに含まれるスペクトル（周波数）エネルギーを分析することです。その他の応用には、畳み込み （線形システム応答）、デジタルフィルタリング、相関（時間遅延推定、類似度測定）、時間周波数解析の高速計算が含まれます。

この変換の高速版である高速フーリエ変換（FFT）は、Cooley と Tukey [2] によって最初に開発され、その後「混合基数」アルゴリズムによって、さらに高速化とさまざまなデータ長での使用が可能になりました。Igor Pro® は、高速多次元素因数分解 Cooley-Tukey アルゴリズムを使って FFT を計算します。

フーリエ変換は数学的に複雑ですが、Igor Pro のフーリエ変換ダイアログを使えば簡単に操作できます。

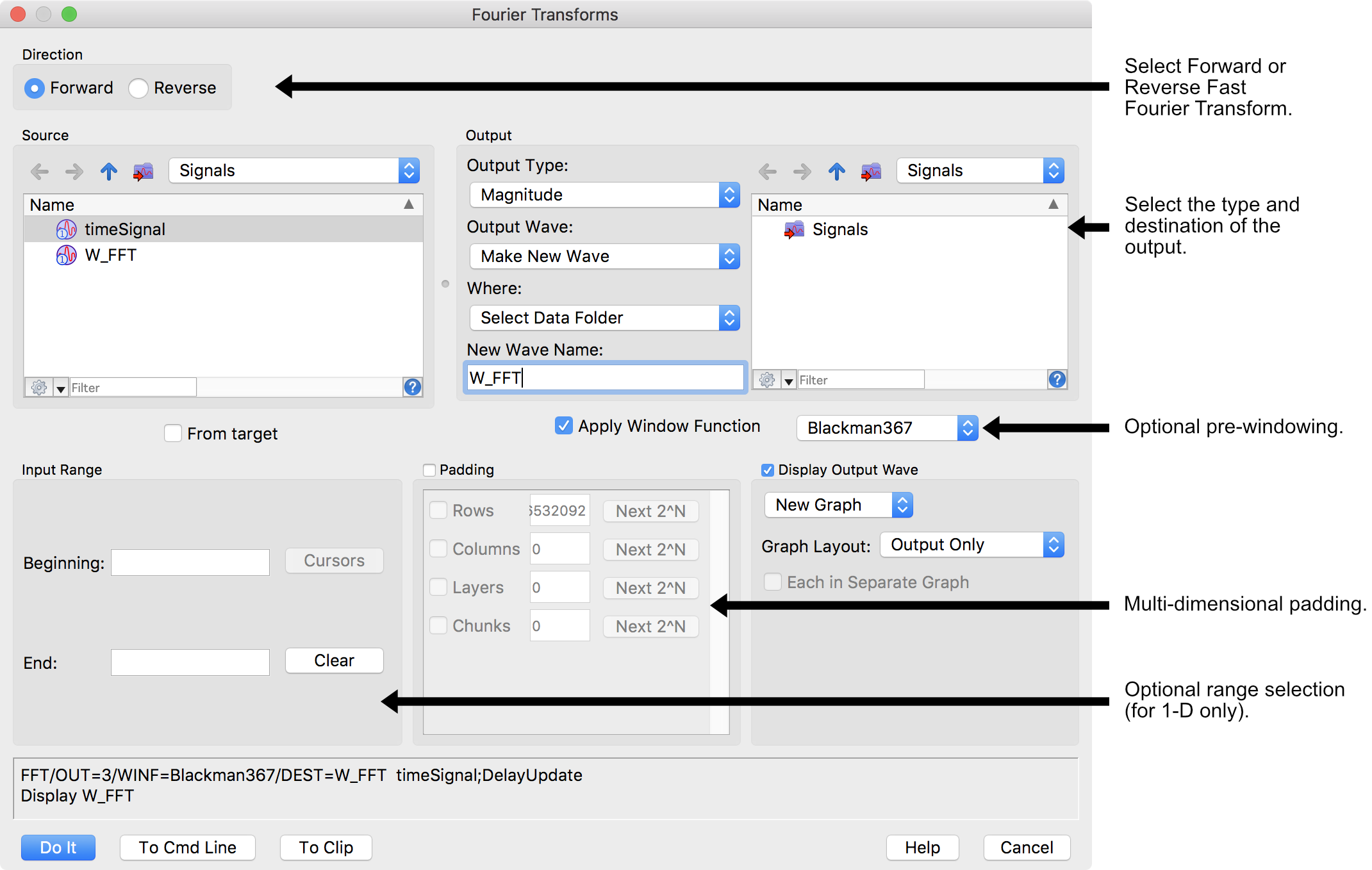
Igor Pro の FFT 演算は高度な計算をサポートしており、その一部は Fourier Transforms ダイアログの以上のものがあります：

• ２次元、３次元、および４次元データの FFT
• 入力データの長さのパディング
• 入力データのウインドウ処理
• 複素数、実数のみ、虚数のみ、絶対値、絶対値の二乗、または位相としての結果
• 超複素正弦変換
• 超複素余弦変換

FFT に加えて、Igor Pro は以下の変換を提供します：

• ピリオドグラム
• Lomb ピリオドグラム
• MultiTaperPSD
• 離散ウェーブレット変換（DWT）
• 連続ウェーブレット変換（CWT）
• Wigner 変換
• 短時間フーリエ変換
• Hilbert 変換

参考文献

1. G.D. Bergland, “A guided tour of the fast Fourier transform,” IEEE Spectrum 7, 41-52 (1969).
2. James W. Cooley and John W. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Math. Comput. 19, 297-301 (1965).