
ノイズ関数
以下の関数は、指定された形状とパラメーターを持つ擬似乱数分布から数値を返します。enoise と gnoise では乱数生成器を選択するオプションがありますが、その他のノイズ関数では初期の均一擬似乱数分布に Mersenne Twister アルゴリズムを使います。再現性のある結果が必要な場合は、いずれのノイズ関数を実行する前にも SetRandomSeed を使うべきであることに注意してください。
組み込みのノイズ関数と分布
| ノイズ関数 | 分布 |
| binomialNoise | 二項分布 |
| enoise | 一様分布 |
| expNoise | 指数分布 |
| gammaNoise | ガンマ分布 |
| gnoise | ガウス分布 |
| HyperGNoise | 超幾何分布 |
| logNormalNoise | 対数正規分布 |
| poissonNoise | ポアソン分布 |
| StatsPowerNoise | パワー分布 |
| StatsVonMisesNoise | フォン・ミーゼス分布 |
| WNoise | 2パラメーター・ワイブル分布 |
様々なノイズ関数が確かに目的の分布を生成することを簡単に確認できます。例えば、次のようにガンマ分布から 10000 個のデータポイントを生成したと仮定します:
Make/O/N=1e4 noiseWave=gammaNoise(10,2)
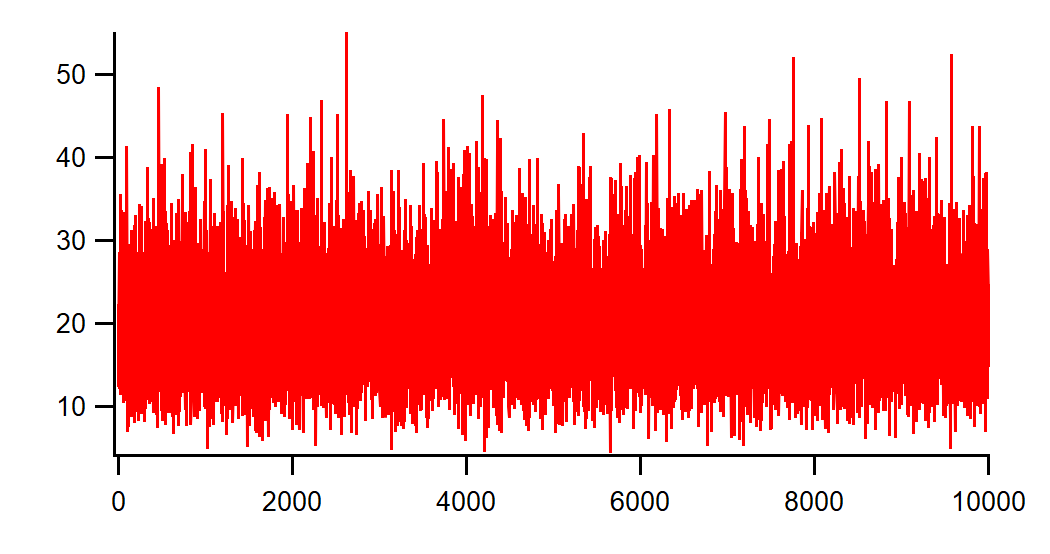
Make/O/N=100/O W_Hist Histogram/P/B={0,1,100} noiseWave,W_Hist
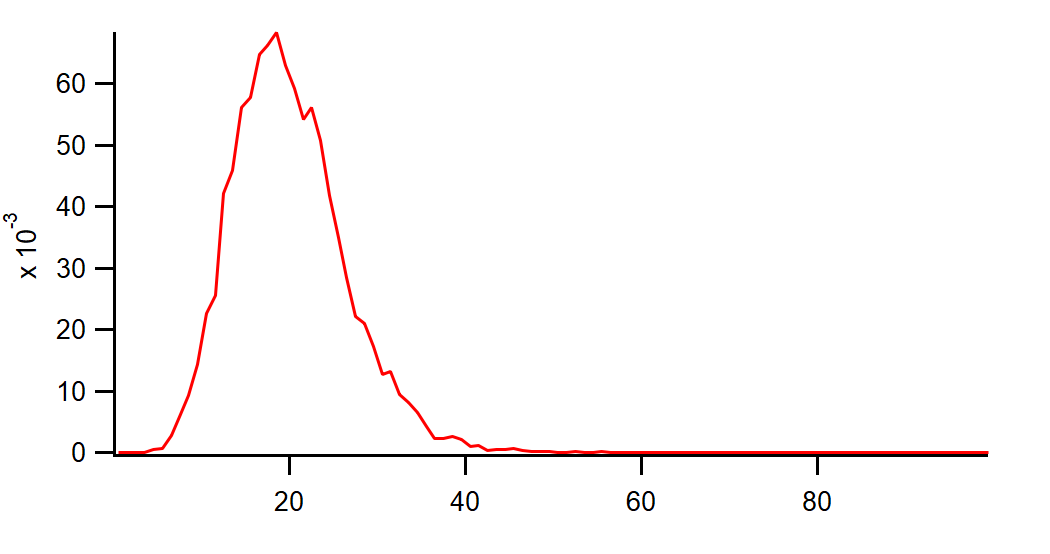
これをガンマ分布にフィッティングさせるため、以下のユーザー関数を記述します:
Function myFit(w,x) : FitFunc Wave w Variable x return x^(w[0]-1)*exp(-x/w[1])/((w[1]^w[0])*Gamma(w[0])) End
フィッティング係数の初期推定値を決定するため、noiseWave の平均値が 19.8681 であることを確認します。この平均値はガンマ分布の2つのパラメーターの積 a*b に等しいはずです。したがって推定値は a=b=sqrt(19.8) となります。
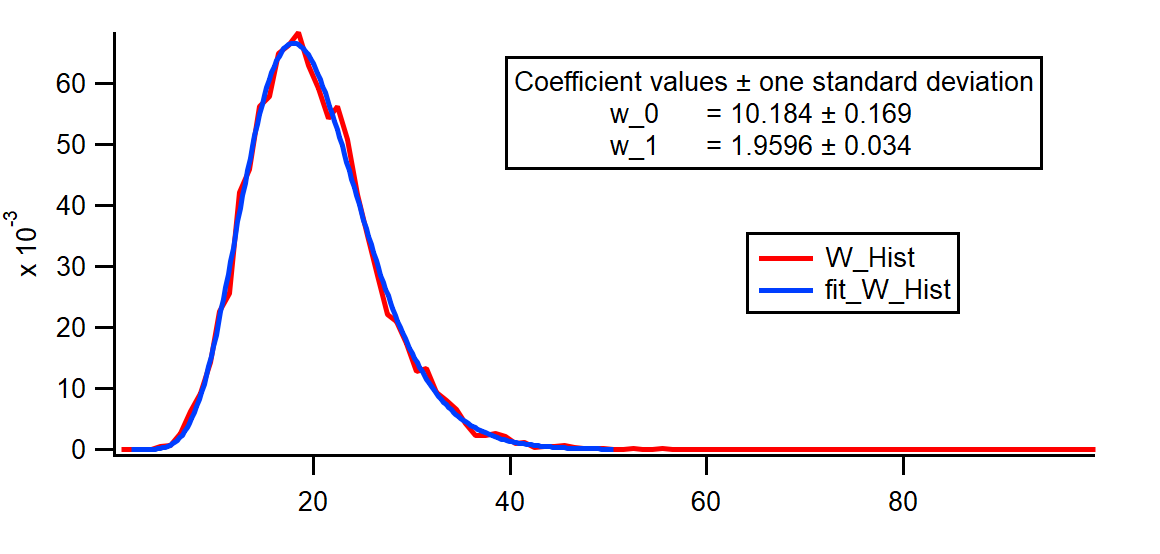
Make/O/D/N=2 W_coef={4.48,4.48} FuncFit/NTHR=0/TBOX=768 myFit W_coef W_Hist[1,50] /D
ガンマ分布へのフィッティング結果は、計算された分布(赤)の上にプロットされ、下のように青色で示されます。

Forum

Support

Gallery
Igor Pro 10
Learn More
Igor XOP Toolkit
Learn More
Igor NIDAQ Tools MX
Learn More