時間周波数解析

時間周波数解析

時間周波数解析は、通常、一定時間間隔でスペクトルを計算することにより、様々な信号周波数が存在する時間を特定します。

ソノグラム

「短時間フーリエ変換」とも呼ばれるソノグラムは、時間ウィンドウをスライドさせながらフーリエスペクトルを計算することで生成される二次元画像です。

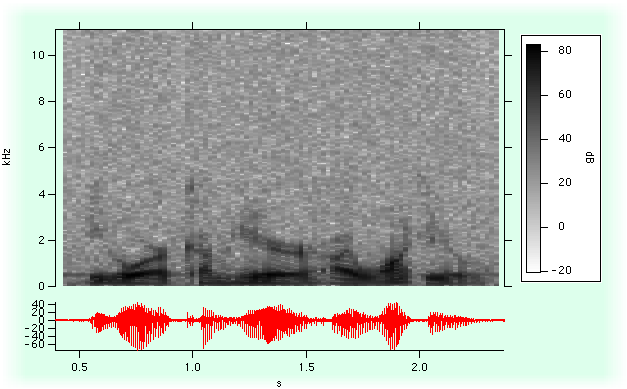
ウィンドウの幅を調整することで、得られるスペクトルの時間分解能を決定できます。

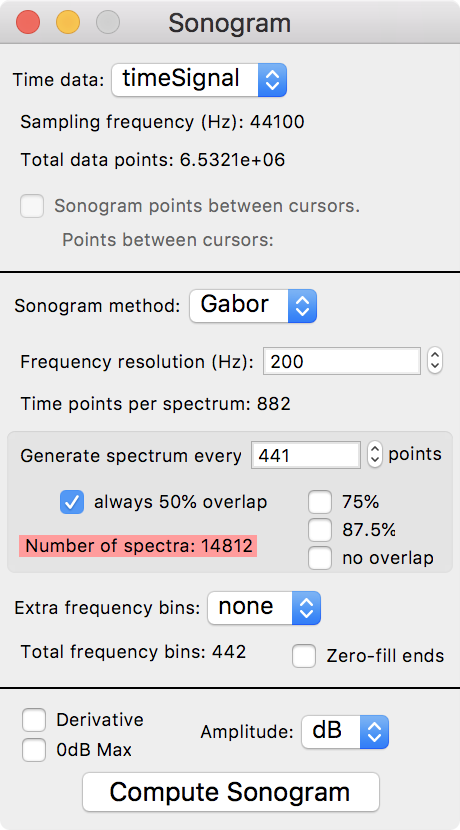
Wigner 変換

Wigner 変換（Wigner 分布関数または WDF とも呼ばれます）は、１次元時間信号 U(t) を２次元時間周波数表現に変換します。概念的には、WDF は時間軸を水平方向に、周波数（音符）を垂直方向にプロットした楽譜に類似しています。WDF は次の式で定義されます。

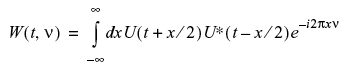
WDF W(t, ν) は実数であることに注意してください（これは、それが Hermitian 量のフーリエ変換であるという事実からわかります）。WDF はまた、Ambiguity 関数の２次元フーリエ変換でもあります。局所化されたスペクトルは、有限領域 ∂t∂ν 上で WDF を積分することで導出できます。t と ν の両方にガウス重み関数を用い、最小不確定条件 ∂t∂ν=1 を選択することで、局所スペクトルの推定値を得ます。

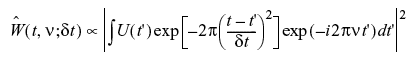
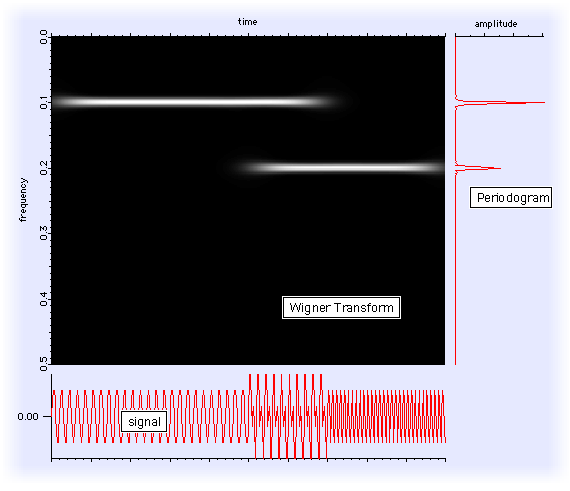
WignerTransform コマンドの応用例として、２周波数の信号、その Wigner 変換、およびそのピリオドグラムを考えてみます。

• Make/N=500 signal
  signal[0,350]=sin(2*pi*x*50/500)
  signal[250,]+=sin(2*pi*x*100/500)
  WignerTransform /Gaus=100 signal
  DSPPeriodogram signal // spectrum for comparison
  

連続ウェーブレット変換

連続ウェーブレット変換（Continuous Wavelet Transform:CWT）は、信号の時間周波数表現であり、図形的には Wigner 変換と表面的な類似性を持っています。

ウェーブレット変換は、信号 s(t) と、基底関数の並進および拡大によって生成される関数群との畳み込みです。基底関数はマザーウェーブレットと呼ばれ、並進または拡大された関数はウェーブレットと呼ばれます。数学的には、CWT は次の式で与えられます。

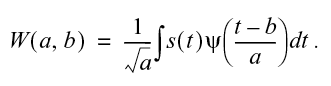
ここで b は時間変換であり、a はウェーブレットの拡大です。

計算上の観点から、畳み込みを計算するために FFT を用いるのは自然であり、これは結果が s(t) の適切なサンプリングに依存していることを示唆しています。

マザーウェーブレットが複素数の場合、CWT も複素数値関数となります。それ以外の場合は CWT は実数値となります。CWT の二乗振幅 |W(a,b)|^² はパワースペクトルと同等であるため、CWT の典型的な表示（画像）は時間オフセット b の関数としてのパワースペクトルの表現となります。ただし、CWT の正確な形式はマザーウェーブレット y の選択に依存するため、CWT の二乗振幅とパワースペクトルとの等価性の程度は応用分野によって異なることに留意すべきです。

CWT 演算は FFT と離散和アプローチの両方を使って実装されます。デルタ関数を入力として用いることで、有効ウェーブレットの表現を得るためにいずれか一方を使用できます。

CWT の例

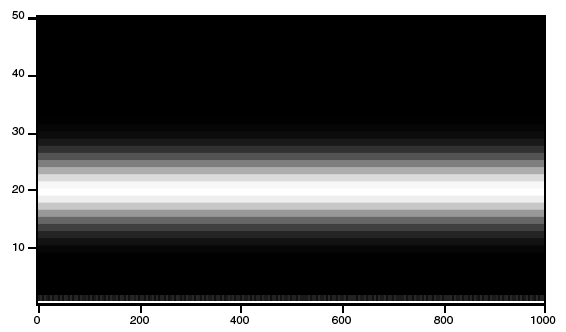
• Make/O/N=1000 signal=sin(2*pi*x*50/1000)	// test signal is simple sine wave
  CWT/OUT=4/SMP2=1/R2={1,1,40}/WBI1=MorletC/FSCL/M=1/ENDM=2 signal
  

画像として表示された２次元 M_CWT の結果：

離散ウェーブレット変換

離散ウェーブレット変換（Discrete Wavelet Transform:DWT）は、フーリエ変換と同様に、信号を基底関数セットを用いて分解する手法です。フーリエ変換では基底関数セットは正弦関数と余弦関数で構成され、展開は単一のパラメーターを持ちます。ウェーブレット変換では展開は２つのパラメーターを持ち、関数（ウェーブレット）は１つの「マザーウェーブレット」から、２つのパラメーターに対応する拡張（ディレーション）とオフセットを用いて生成されます。

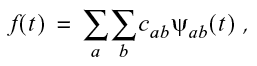
ここで、２パラメーター展開係数は次のように与えられます。

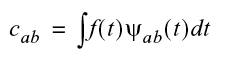
そしてウェーブレットは次の条件に従います。

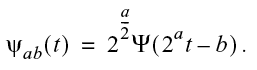
ここで Ψ はマザーウェーブレット、a は拡張パラメーター、b はオフセットパラメーターです。

２つのパラメーターによる表現は、１次元信号からより高い次元へと移行するにつれて、事態を急速に複雑にする可能性があります。さらに、各スケールにおける係数の数は 2 の累乗として変化するため、１次元信号の DWT は（CWT の場合のように）２次元画像として便利に表現することはできません。したがって、変換の結果は、入力と同じ次元数になるように「パック」するのが通例です。例えば、入力が 128 ポイント（=2⁷）の１次元ウェーブの場合、有効なスケールは 7-1=6 つあり、以下のように配置されます。

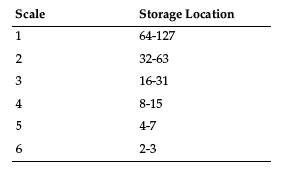
DWT の定義から導かれる興味深い結果として、デルタ関数の適切な形を逆変換することでウェーブレットの形状を特定できることが挙げられます。例えば、

• Make/N=1024 delta=0
  delta[22]=1
  DWT/I delta
  Display W_DWT // Daubechies 4 coefficient wavelet
  

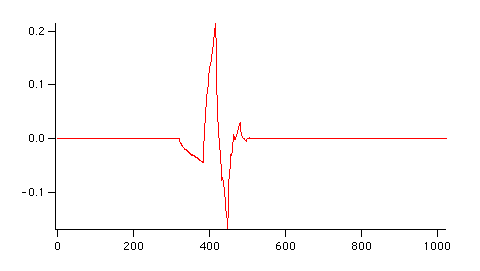
DWT 基底関数の重要な点は、特定の持続時間外では正確にゼロになることです。これは、基底関数が無限の正弦ウェーブであるフーリエ変換とは異なります。

この差が、DWT のより一般的な応用の一つである「ノイズ除去」の基礎となっています。

DWT によるノイズ除去

DWTを用いた信号の「ノイズ除去」には、以下の３つのステップが含まれます：

1. 入力信号を DWT で変換する
2. 変換係数の絶対値が、変換の最大絶対値の何パーセントかに満たないものをすべてゼロにする
3. 逆 DWT を行う

Wavelet Demo Example エクスペリメントがこのテクニックを示しています。

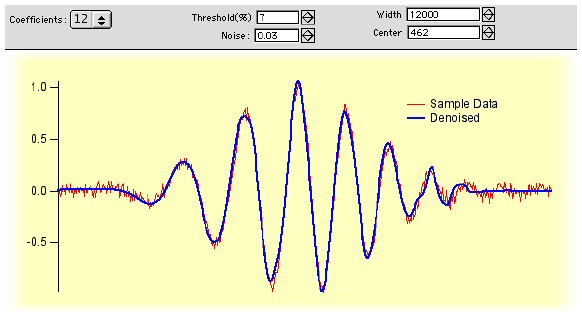
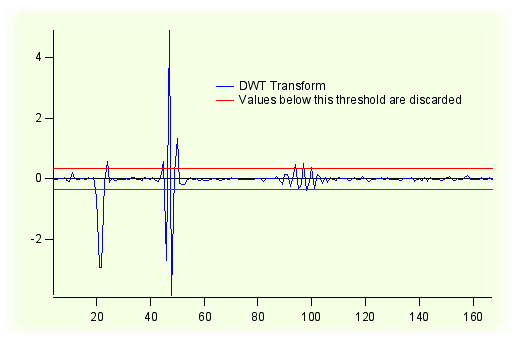
Igor Pro® の DWT 演算は、/D フラグが指定された場合にノイズ除去処理を実行します。

参考文献

• Wigner, E. P., On the quantum correction for thermo-dynamic equilibrium, Physics Review, 40, 749-759, 1932.
• Bartelt, H.O., K.-H. Brenner, and A.W. Lohman, The wigner distribution function and its optical production, Optics Communications, 32, 32-38, 1980.
• Torrence, C., and G.P. Compo, A Practical Guide to Wavelet Analysis, Bulletin of the American Meteorological Society, 79, 61-78, 1998.