Kolmogorov-Smirnov Distribution

Igor’s StatsKSTest performs the Kolmogorov–Smirnov (KS) goodness‑of‑fit test for comparing two continuous distributions. The operation was originally implemented in the early 2000s so its reported critical values and p‑values are based on legacy algorithms. Unfortunately, the older algorithms have several known deficiencies that should be corrected. This topic is discussed in detail in:

Simard, R., & L’Ecuyer, P. (2011). Computing the Two-Sided Kolmogorov–Smirnov Distribution. Journal of Statistical Software, 39(11), 1–18.

https://doi.org/10.18637/jss.v039.i11

https://www.iro.umontreal.ca/~lecuyer/myftp/papers/ksdist.pdf

A good overview of the complexity of calculating the distribution function is provided in Figure 2 of the article.

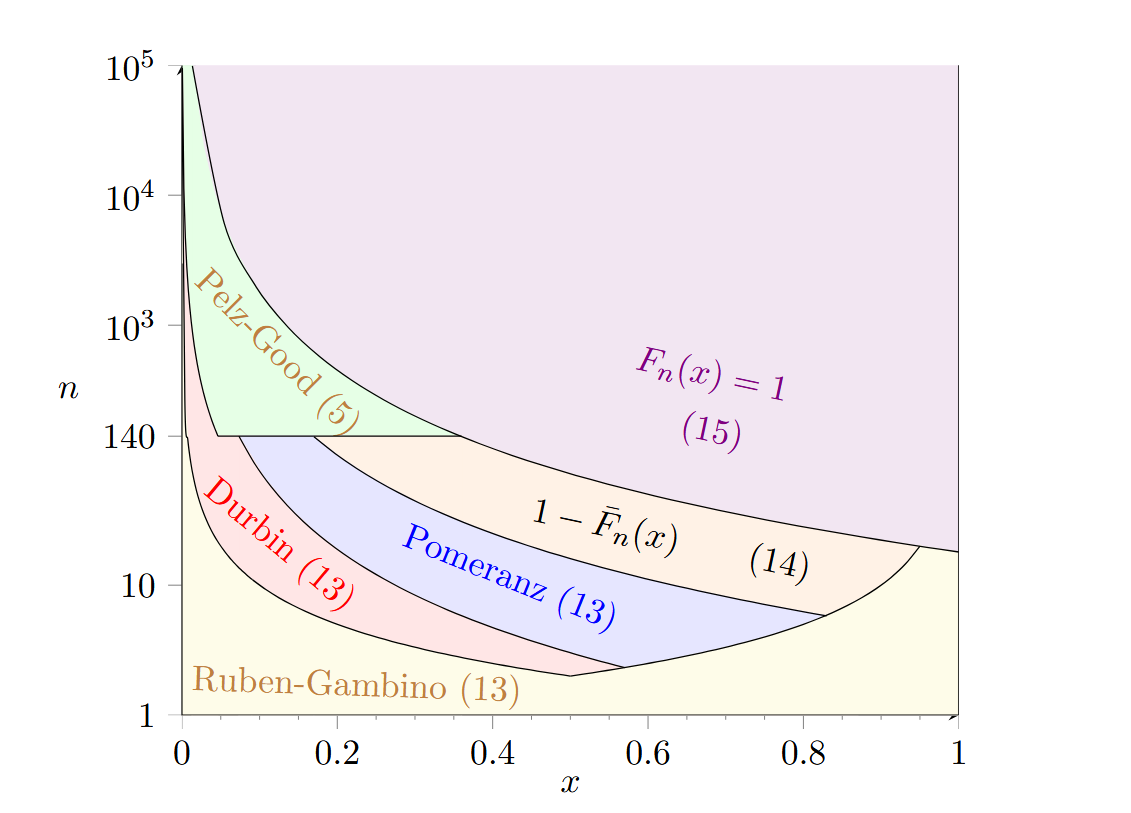
Figure 2: Choice of method to compute (or approximate) Fn(x) and minimal number of
decimal digits of precision for Fn(x), as a function of (n, x), in each region of N × [0, 1].

Reproduced from Simard, R., & L’Ecuyer, P. (2011). Computing the Two-Sided Kolmogorov–Smirnov Distribution. Journal of Statistical Software, 39(11), 1–18. https://doi.org/10.18637/jss.v039.i11. Licensed under CC‑BY.

This domain segmentation is implemented in the C code accompanying the article. Included here is an Igor procedure derived from that published code. A small number of modifications were required for the conversion, and these are listed at the top of the procedure. The procedure code is provided as is and it remains subject to the original copyright and licensing terms.

The procedure supports the following functions:

KScdf(int n,double x) - returns the Kolmogorov-Smirnov CDF.
getKSCritical(variable n,variable alpha) - returns the critical value for the Kolmogorov-Smirnov distribution.

Please send comments or questions to support@wavemetrics.com.

A.G.